如果方程F(x,y)=0能確定y是x的函式,那么稱這種方式表示的函式是隱函式。而函式就是指:在某一變化過程中,兩個變數x、y,對於某一範圍內的x的每一個值,y都有確定的值和它對應,y就是x的函式。這種關係一般用y=f(x)即顯函式來表示。F(x,y)=0即隱函式是相對於顯函式來說的。
基本介紹
- 中文名:隱函式
- 外文名:implicit function
- 套用學科:高等數學
- 適用領域範圍:數學分析
- 分類:數學
- 相關名詞:函式
定義
求導法則
推理過程



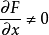
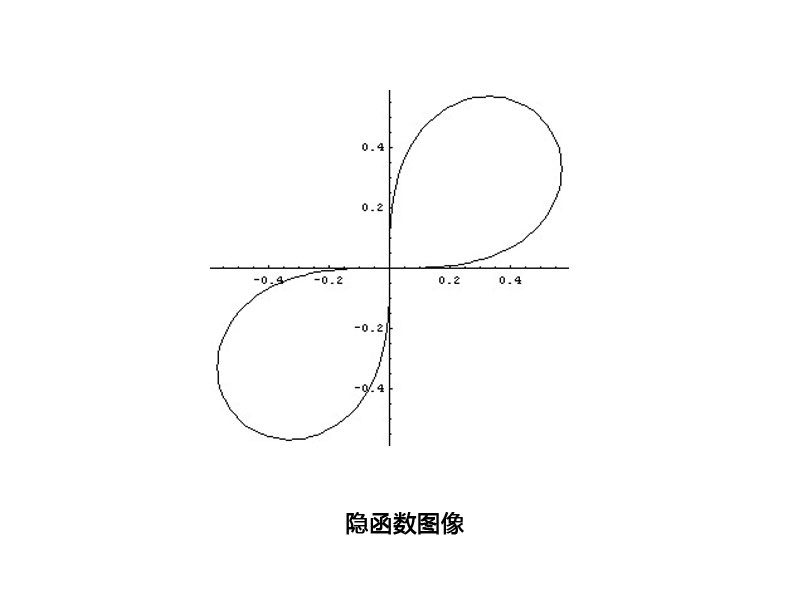
如果方程F(x,y)=0能確定y是x的函式,那么稱這種方式表示的函式是隱函式。而函式就是指:在某一變化過程中,兩個變數x、y,對於某一範圍內的x的每一個值,y都有確定的值和它對應,y就是x的函式。這種關係一般用y=f(x)即顯函式來表示。F(x,y)=0即隱函式是相對於顯函式來說的。



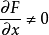
如果方程F(x,y)=0能確定y是x的函式,那么稱這種方式表示的函式是隱函式。而函式就是指:在某一變化過程中,兩個變數x、y,對於某一範圍內的x的每一個值,y都...
在數學中,隱函式定理是一個描述關係以隱函式表示的某些變數之間是否存在顯式關係的定理。隱函式定理說明,對於一個由關係R(x,y)=0表示的隱函式,如果它在某一點...
因變數與自變數之間的對應法則是由一個方程式所確定的形式稱為隱函式,由多個隱函式組成的方程組稱為隱函式組...
《隱函式和解映射(英文)》在經典框架及其外研究隱函式的本質,主要側重於研究變分問題解映射的性質。《隱函式和解映射(英文)》自稱體系,並將大量散落的材料綜合起來...
顯函式是函式的類型之一,解析式中明顯地用一個變數的代數式表示另一個變數時,稱為顯函式。...
反函式組是函式的另一種表現形式,反函式組的存在性問題是隱函式組存在性問題的一種特殊形式。反函式組是數學分析領域函式理論方面的重要內容。...
函式的定義:給定一個數集A,假設其中的元素為x。現對A中的元素x施加對應法則f,記作f(x),得到另一數集B。假設B中的元素為y。則y與x之間的等量關係可以用y...
在數學中,反函式定理給出了向量值函式在含有定義域中一點的開區域內具有反函式的充分條件。該定理還說明了反函式的全導數存在,並給出了一個公式。反函式定理可以...
若變數x,y之間的函式關係是由一個方程F(x,y)=0所確定,則稱這種函式為隱函式,隱微分法是指:不從方程F(x,y)=0中解出y,而把y看成是x的函式,在方程兩邊...
一階微分形式不變性是指:無論u,v是自變數還是中間變數,函式z=f(u,v)的全微分形式是一樣的。此性質的好處是:一方面是可以不用區分變數直接利用一元函式的微分...
5.掌握多元複合函式一階、二階偏導數的求法.6.了解隱函式存在定理,會求多元隱函式的偏導數.7.了解空間曲線的切線和法平面及曲面的切平面和法線的概念,會求它們...
求導是數學計算中的一個計算方法,它的定義就是,當自變數的增量趨於零時,因變數的增量與自變數的增量之商的極限。在一個函式存在導數時,稱這個函式可導或者可微分...
這方程可以寫成x3y2=c,它定義的隱函式滿足原來的微分方程。高階方程也可以稱為恰當方程,如果它是一個較低階的方程微分的結果。例如,二階方程p(x)y″+q(x)...
鏈式法則是微積分中的求導法則,用於求一個複合函式的導數,是在微積分的求導運算中一種常用的方法。複合函式的導數將是構成複合這有限個函式在相應點的 導數的乘積...
主要包括三個部分:Banach空間微分學(連續、有界、導數、全連續、微分方程與Hamiltoin系統的變分學框架、隱函式定理、分歧與約化)拓撲度及錐理論(Brouwer度、L-S...
