基本介紹
- 中文名:微分形式
- 外文名:differential form
- 性質:多變數微積分
- 提出者:埃里·卡當
- 適用範圍:數理科學
定義
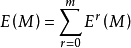
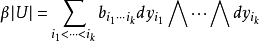
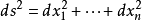
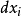

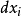
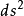
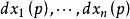
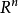
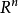
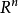

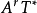

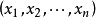
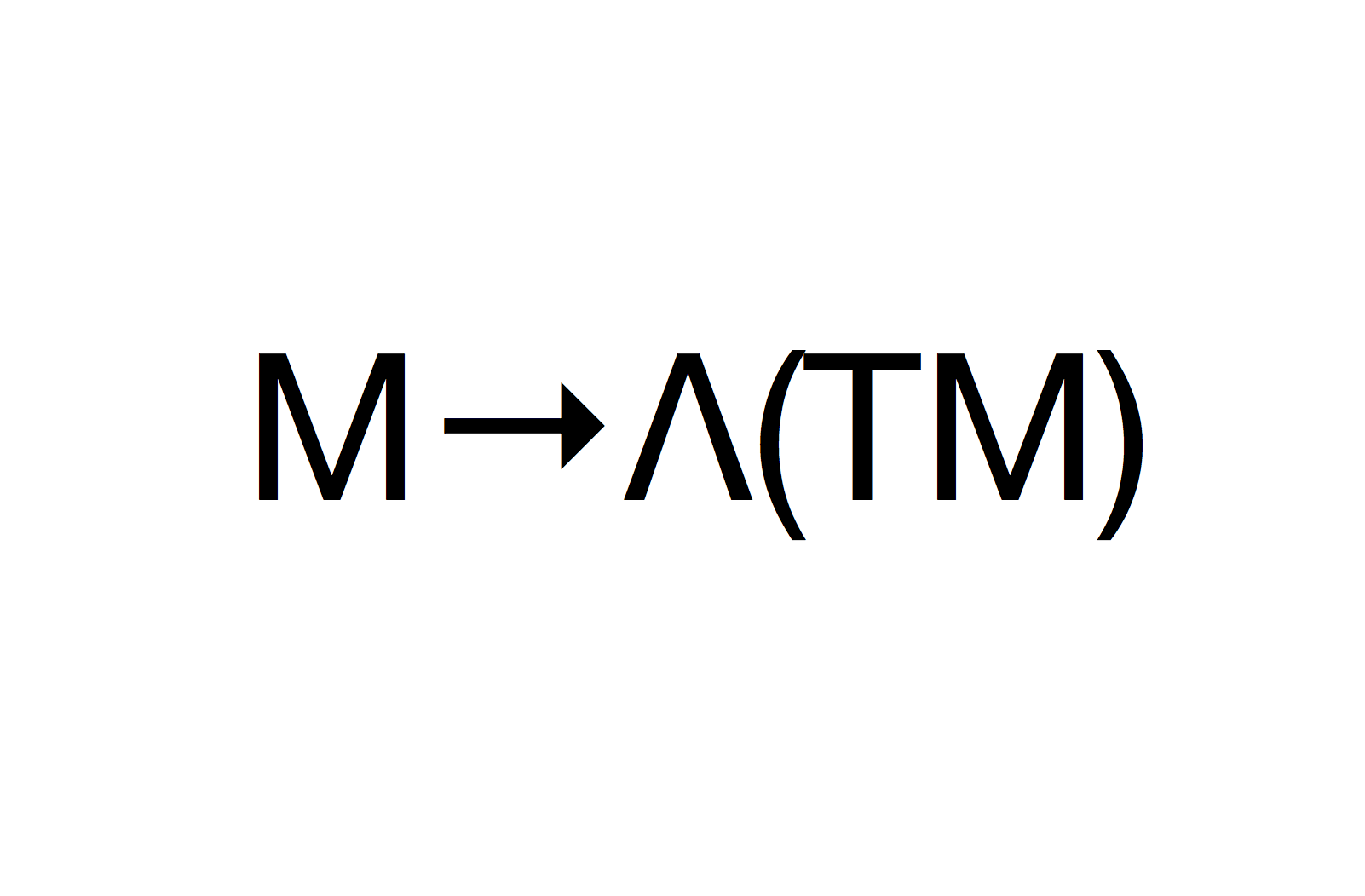
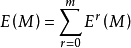
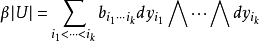
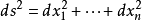
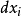

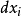
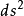
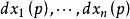
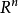
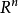
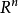

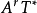

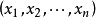
微分形式(differential form)是多變數微積分,微分拓撲和張量分析領域的一個數學概念。現代意義上的微分形式,及其以楔積和外微分結構形成外代數的想法,都是由著名法國...
外微分形式,又稱微分形式,是微分流形上定義的反對稱協變張量場。...... 外微分形式,又稱微分形式,是微分流形上定義的反對稱協變張量場。中文名 外微分形式 ...
《微分形式及其套用》是2010年世界圖書出版公司出版的圖書,作者是(巴西)杜卡莫。本書詳細講述了微分幾何,並運用它們研究曲面微分幾何的局部和全局知識。...
《數學物理中的微分形式》是1989年北京航空航天大學出版社出版的一本圖書,作者是韋斯坦霍爾斯(Westenholz,C.V.)。...
書名:微分形式——理論與練習作者: 溫特勞斯責編:張永芹I S B N:978-7-5603-5518-4定價:58.00元出版日期:2015.08開本:16頁數:407...
數學中,流形 M 上一個向量值微分形式(vector-valued differential form)是 M 上取值於一個向量空間 V 的微分形式。更一般地,它是取值於 M 上某個向量叢 E ...
在數學中,微分是對函式的局部變化率的一種線性描述。微分可以近似地描述當函式自變數的取值作足夠小的改變時,函式的值是怎樣改變的。當某些函式f的自變數x有一個...
恰當形式(exact differential form)是一類微分形式,可成為另一個外微分形式的外微分的微分形式。...
外微分為零的外微分形式,即,滿足dω=0的外微分形式ω稱為閉形式(closed differential form)。...
《代數拓撲中微分形式》是2009年世界圖書出版社出版的圖書,作者是(美國)RaoulBott(美國)LoringW.Tu。...
微分流形(differentiable manifold),也稱為光滑流形(smooth manifold),是拓撲學和幾何學中一類重要的空間,是帶有微分結構的拓撲流形。 微分流形是微分幾何與微分...
叢ΛpCT*(M)的截面就稱為M上的復微分p形式(complex differential p-form),p≥0。...... 叢ΛpCT*(M)的截面就稱為M上的復微分p形式(complex differential p...
