隱函式存在定理主要講述如何從二元函式F(x,y)的性質來判定由F(x,y)=0所確定的隱函式y=f(x)是存在的,並且,這個函式還具有某些特性。
基本介紹
- 中文名:隱函式存在定理
- 外文名:The implicit function existence theorem
- 學科:數學
- 類型:數學定理
- 釋義:判定隱函式存在的條件
- 條件:充分條件
隱函式

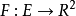














隱函式定理
存在唯一性定理

























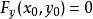

可微性定理





n元隱函式





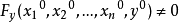















隱函式組


























隱函式存在定理主要講述如何從二元函式F(x,y)的性質來判定由F(x,y)=0所確定的隱函式y=f(x)是存在的,並且,這個函式還具有某些特性。

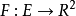







































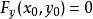











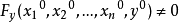









































隱函式存在定理主要講述如何從二元函式F(x,y)的性質來判定由F(x,y)=0所確定的隱函式y=f(x)是存在的,並且,這個函式還具有某些特性。...
隱函式存在定理就用於斷定(3)就是這樣的一個條件,不僅必要,而且充分。隱函式示例 編輯 設方程P(x, y)=0確定y是x的函式,並且可導。如今可以利用複合函式求導...
全書共分三冊,本書為第三冊,分為8章:多元函式的極限與連續性、多元函式微分學、隱函式存在定理、一般極值與條件極值、含參變數的積分、重積分、曲線積分與曲面...
隱函式存在定理是微積分中的難點,一般的教材介紹這一部分時,儘管對定理的證明不做要求,但是推導偏導數的過程複雜,公式繁多,導致許多學生在求隱函式的偏導數時,常...
例如對微分中值定理的推廣;多變數函式一致連續性的判定定理;隱函式存在定理以及其可微性定理的證明;部分可微但整體不可微的函式的例子;多變元函式泰勒展開的條件;...
(下)為下冊,內容包括數項級數和廣義積分;函式項級數、冪級數、富里埃級數和富里埃變換,多元函式的極限與連續、偏導數和全微分、極值理論、隱函式存在定理與函式...
滿足隱函式存在定理的條件,則有 ,並且曲面的面積可表示為很顯然,當給定不同的 時,面積S是不同的。曲面面積是關於函式 的函式,稱面積S是函式 的泛函.函式 必須...
7.4 隱函式定理 1977.4.1 隱函式存在定理 1977.4.2 隱函式的可微性定理 1997.4.3 舉例 2007.5 泛函極值問題 2027.5.1 泛函極值的必要條件 202...
,則由隱函式存在定理,在點( , , )附近由該方程可以確定 y=y(x),z=z(x),其中 =y( ), =z( ),它是這個曲線方程的參數形式。將...
10.3 知識點3:隱函式存在定理及其套用 10.3.1 要點歸納 10.3.2 例題解析 第11章 多變數積分學 11.1 知識點1:重積分 11.1.1 要點歸納 11.1.2 例題...
本書加強了對基本概念的分析訓練,同時著重介紹定理和例題證明的分析思路。...14.5 隱函式存在定理14.5.1 隱函式存在定理14.5.2 反函式組的存在性習題...
由隱函式存在定理可知,在 對連續可微的前提下,只須 便足以保證 也對 連續可微。這樣,連續可微函式組便在雅可比行列式不等於零的條件之下,在每一對相應點u與x...
二、函式行列式的性質三、函式行列式的幾何性質 [3] 練習題11.211.3 條件極值一、條件極值與拉格朗日乘數法二、例練習題11.311.4 隱函式存在定理在幾何方面的...
5.掌握多元複合函式一階、二階偏導數的求法.6.了解隱函式存在定理,會求多元隱函式的偏導數.7.了解空間曲線的切線和法平面及曲面的切平面和法線的概念,會求它們...
5.掌握多元複合函式一階、二階偏導數的求法.6.了解隱函式存在定理,會求多元隱函式的偏導數.7.了解空間曲線的切線和法平面及曲面的切平面和法線的概念,會求它們...
第五節隱函式的求導法則72一、 一元隱函式存在定理和隱函式的求導公式72二、 二元隱函式存在定理和隱函式的求導公式73習題8 574第六節多元函式微分學的幾何套用...
§10.4 二元函式的泰勒公式第十一章 隱函式知識結構圖§11.1 隱函式的存在性§11.2 函式行列式§11.3 條件極值§11.4 隱函式存在定理在幾何方面的套用...
第12章 傅立葉級數第13章 多元函式的極限與連續第14章 偏導數和全微分第15章 極值和條件極值第16章 隱函式存在定理---函式相關第17章 含參變數的積分...
3. 了解多元函式偏導數與全微分的概念,會求多元複合函式一階、二階偏導數,會求全微分,了解隱函式存在定理,會求多元隱函式的偏導數....
5.掌握多元複合函式一階、二階偏導數的求法.6.了解隱函式存在定理,會求多元隱函式的偏導數.7.了解空間曲線的切線和法平面及曲面的切平面和法線的概念,會求它們...
17.1 多元函式的極限和連續17.2 Euclid空間上的映射17.3 連續映射第十八章 偏導數18.1 偏導數和全微分18.2 鏈式法則第十九章 隱函式存在定理和隱函式求導法...
《數學分析理論及套用》共分12章,主要內容包括函式、極限與連續;導數與微分;微分基本定理及其套用;不定積分;定積分及其套用;數項級數;函式項級數;多元函式的極限與...
