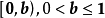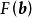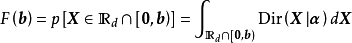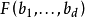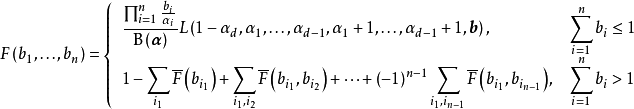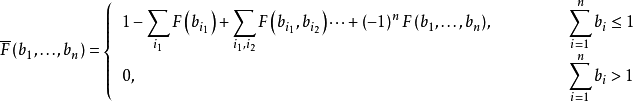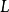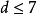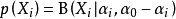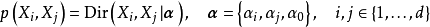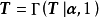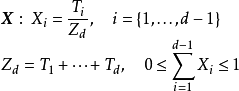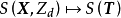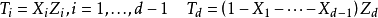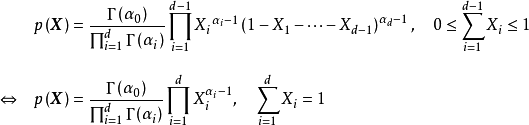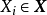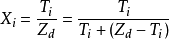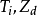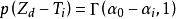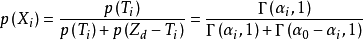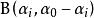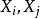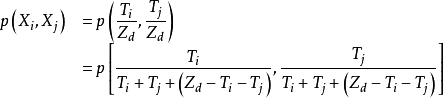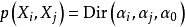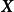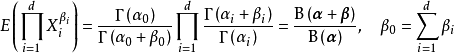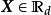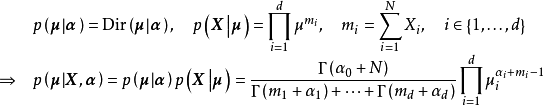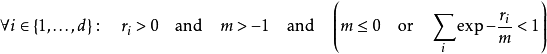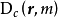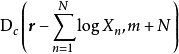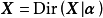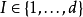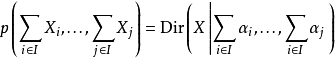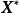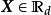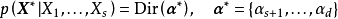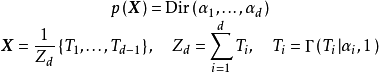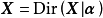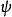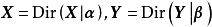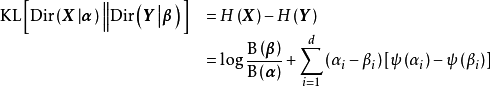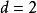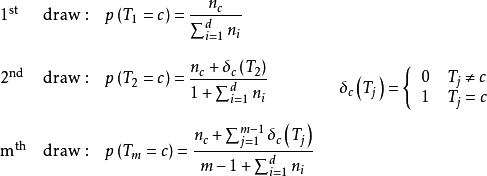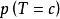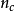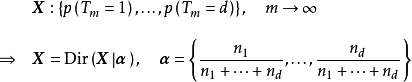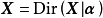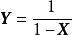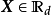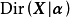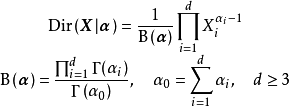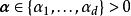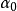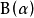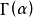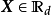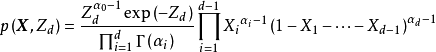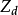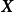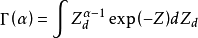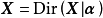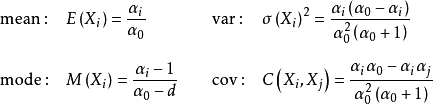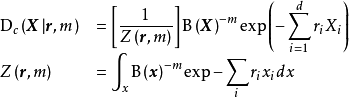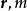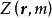歷史
(式中符號按Gupta and Richards, 2001)同年,狄利克雷的好友,法國數學家約瑟夫·劉維爾(Joseph Liouville)完善了狄利克雷的推導並將其推廣得到了更一般形式的積分,該積分被稱為劉維爾積分,是劉維爾分布的積分形式。
狄利克雷積分出現後,在十九世紀沒有得到學界的關注。二十世紀初,Louis Bachelier將狄利克雷分布視為
多項分布的共軛先驗進行了研究。
卡爾·皮爾遜(Karl Pearson)及其合作者得到了狄利克雷分布的
邊緣分布、
條件分布和
矩。George Pólya通過推導多元分布變數的相對頻率的
極限分布得到了狄利克雷分布。此後狄利克雷分布在
貝葉斯推斷、多元變數建模等問題中的套用逐漸得到重視。1962年,英國數學家Samuel Wilks在其著作Mathematical statistics中首次使用“狄利克雷分布”一詞描述其機率密度函式,並將其與狄利克雷的早期工作相聯繫,狄利克雷分布也由此得名。
定義
解析形式
機率密度函式
對獨立同分布(independent and identically distributed, iid)的連續隨機變數
和
支撐集 ,若
服從狄利克雷分布,則其機率密度函式
有如下定義:
式中,
是
無量綱的分布參數,
是分布參數的和,
是多元Beta函式(multivariate beta function),
為
Gamma函式。由上述解析形式可知,狄利克雷分布是
指數族分布。
需要指出,d維iid隨機變數在給定
後僅構成d-1維空間:
,因此上述定義的支撐集等價於:
,此時d維狄利克雷分布的機率密度函式有如下表示:
按幾何觀點,狄利克雷分布的d維支撐集是一個開放的d-1維正單純形(standard simplex),例如3維的狄利克雷分布的支撐集是3維空間內頂點為
的等邊三角形。
狄利克雷分布的一個特例是對稱狄利克雷分布(symmetric Dirichlet distribution),此時分布參數
在所有維度相同,其取值也被稱為濃度參數(concentration parameter)。對稱狄利克雷分布的機率密度函式如下:
對稱狄利克雷分布在每個維度的機率密度是相等的,並由濃度參數決定。當濃度參數為1,即所有維度的分布參數等於1時,d維對稱狄利克雷分布退化為d-1維正單純形上的
均勻分布(uniformed distribution),也被稱為平狄利克雷分布(flat Dirichlet distribution)。當濃度參數大於1時,對稱狄利克雷分布是一個集中分布,此時濃度參數越大,所對應的機率密度越集中;當濃度參數小於1時,對稱狄利克雷分布是一個稀疏分布,此時濃度參數越接近於0,所對應的機率密度越稀疏。
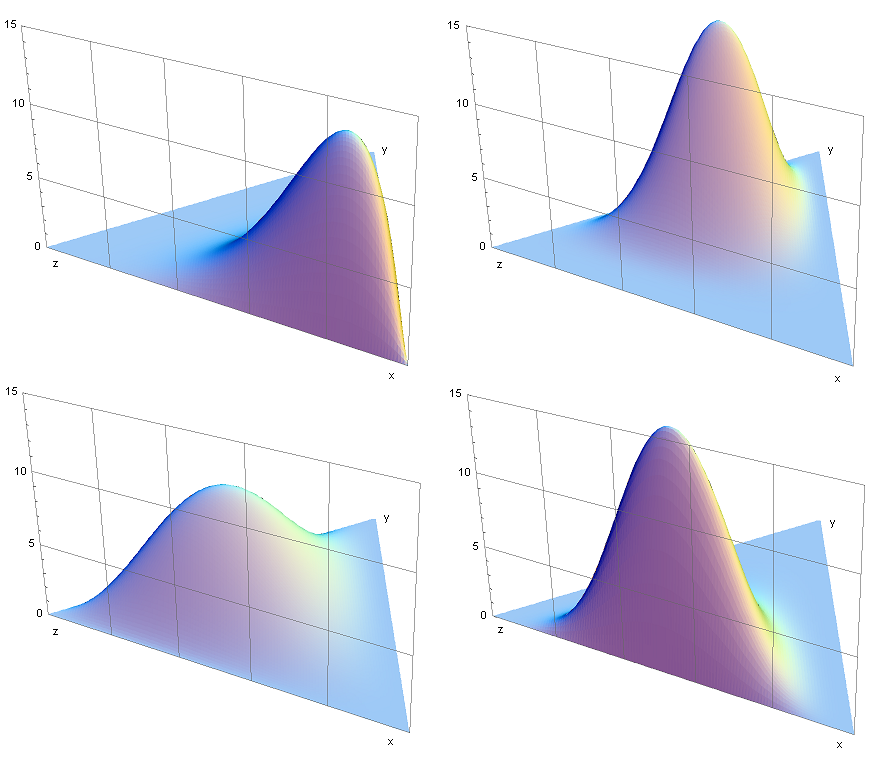
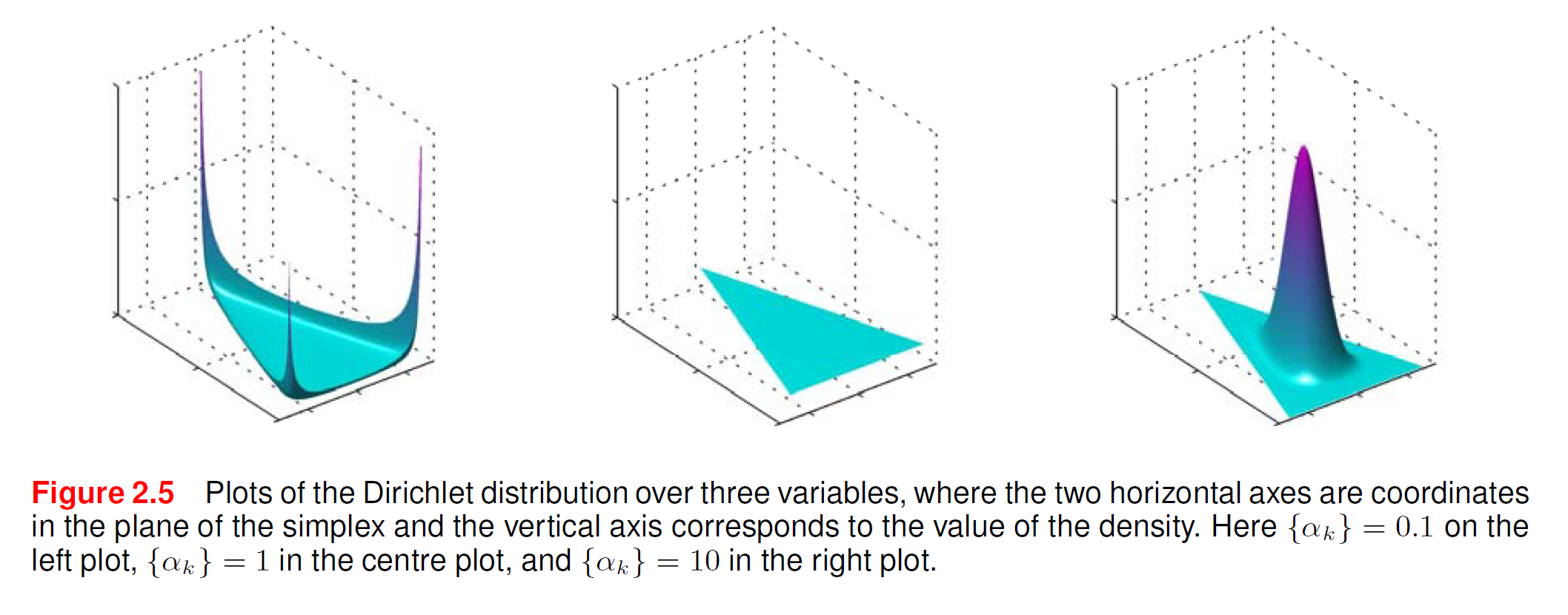 3維對稱狄利克雷分布,左至右:稀疏分布,均勻分布,密集分布
3維對稱狄利克雷分布,左至右:稀疏分布,均勻分布,密集分布積累密度函式
對服從狄利克雷分布的隨機變數
,在
的正交空間下,其積累密度函式
有如下表示:
上述積分可以通過數值模擬,例如採樣方法求解,也可以使用遞歸算法。對於後者,這裡按Gouda and Szántai (2010)做簡單介紹:對
,考慮狄利克雷分布的邊緣分布是Beta分布(參見邊緣分布),因此可按不完全Beta函式(incomplete Beta function)計算所有邊緣分布的積累密度函式
,隨後在每次遞歸中加入一個維度,直到輸出
。對第
次遞歸,更新公式為:
式中
表示Lauricella超幾何函式(Lauricella hypergeometric function)。Lauricella序列展開在高維時計算量大,因此該疊代算法通常用於
的情形。
邊緣分布(marginal distribution)
由上式可知,狄利克雷分布是Beta分布在高維情形下的推廣,或Beta分布是一個2維的狄利克雷分布。
聯合分布(joint distribution)
給定服從狄利克雷分布的隨機變數
,則其兩個邊緣分布
的
聯合分布為狄利克雷分布:
推導
這裡給出狄利克雷分布的機率密度函式、邊緣分布與聯合分布的推導。
給定服從
Gamma分布的d維iid隨機變數
,可得其所有維度的聯合分布有如下形式:
定義新的隨機變數:
現求解該隨機變數的聯合機率密度函式並證明其服從狄利克雷分布。由於間的空間映射
存在單一反函式
,因此由坐標變換法(change of variables)可知,二者的聯合機率分布有如下表示:
求解上述
雅可比行列式(Jacobian determinant)並帶入Gamma分布的解析形式可得:
上式對
積分可得
的聯合機率密度函式,計算時考慮
Gamma函式的解析形式:
:
對邊緣分布,取隨機變數在任意一個維度的分量
,由先前的映射關係可得:
,考慮
均服從Gamma分布,由Gamma分布的可加性:
,因此有:
由Beta分布與Gamma分布的關係,上式右側等價於Beta分布:
。
按先前對狄利克雷分布機率密度函式的推導可得,上式右側為狄利克雷分布,即
。
性質
統計量
對服從狄利克雷分布的隨機變數
,其
均值(mean)、
眾數(mode)、
方差(variance)和
協方差(covariance)有如下表示:
更一般地,
的
矩(moment)可表示為兩個多元Beta函式的比值:
作為機率分布的性質
共軛性(conjugacy)
多項分布(multinomial distribution)的共軛先驗(conjugate piror)是狄利克雷分布,即對狄利克雷分布的先驗,當似然是多項分布時,其後驗分布也為狄利克雷分布。例如給定隨機變數
的N個觀測樣本,則上述性質可表示為:
狄利克雷分布作為多項分布的共軛先驗在貝葉斯推斷中得到了套用。
狄利克雷分布是
指數族分布,因此其共軛先驗也為指數族分布且具有如下形式:
上述分布沒有正式名字,式中的參數
分別為d維向量和標量。
為歸一化常數。在實數域內,當分布參數滿足如下條件時歸一化成立:
在滿足上述條件的支撐集內,給定先驗分布
和狄利克雷分布的似然 ,則後驗分布為
,其中N為樣本數。
聚合性(aggregation property)
狄利克雷分布具有聚合性,對服從狄利克雷分布的隨機變數
,給定其維數對應集合的劃分
,則有:
中立性(neutrality)
服從狄利克雷分布的隨機變數具有完全中立性(complete neutrality),即任意的
都與歸一化後的
相互獨立:
類似於先前機率密度函式的推導,可證明
服從狄利克雷分布。上述性質的重要推論,是狄利克雷分布的聯合條件分布(conditional joint distribution),即若隨機變數
服從狄利克雷分布,則其聯合條件分布有如下表示:
與Gamma分布的關係
由狄利克雷分布機率密度函式的推導可知,對服從Gamma分布的iid隨機變數,其歸一化後的聯合分布是狄利克雷分布:
信息測度
信息熵(Shannon entropy)
信息熵描述了隨機變數的不確定性,或其具有的信息量,對服從狄利克雷分布的隨機變數
,其信息熵有如下表示:
式中
表示雙伽瑪函式(Digamma function),即Gamma函式的對數導數。
相對熵(relative entropy)
相對熵或Kullback-Leibler散度(Kullback-Leibler divergence, KL)是兩個機率分布的非對稱性度量,若有服從狄利克雷分布的隨機變數
,二者的相對熵有如下表示:
此外當
時,狄利克雷分布的信息測度等價於相應的Beta分布的信息測度。
數值模擬
隨機數
狄利克雷分布的隨機數可以由Gamma分布的隨機數歸一化得到。具體地,首先生成尺度參數為1的Gamma分布隨機數,然後對所有隨機數求和,最後按隨機數除以求和結果輸出狄利克雷分布隨機數。這裡給出Python 3環境下上述過程的編程實現:
# 導入模組import numpy as npimport matplotlib.pyplot as pltfrom mpl_toolkits.mplot3d import Axes3D# 生成隨機數alpha = [1, 1, 1] # 三維平狄利克雷分布N = 1000; L = len(alpha) # 樣本數N=1000gamma_rnd = np.zeros([L, N]); dirichlet_rnd = np.zeros([L, N])for n in range(N): for i in range(L): gamma_rnd[i, n]=np.random.gamma(alpha[i], 1) # 逐樣本歸一化(對維度歸一化) Z_d = np.sum(gamma_rnd[:, n]) dirichlet_rnd[:, n] = gamma_rnd[:, n]/Z_d# 繪製散點圖fig = plt.figure()ax = fig.gca(projection='3d')ax.scatter(dirichlet_rnd[0, :], dirichlet_rnd[1, :], dirichlet_rnd[2, :])ax.view_init(30, 60)
Pólya罈子模型
Pólya罈子模型(Pólya urn model)可以模擬狄利克雷分布。
將大於等於3類的d類顏色球放入罈子並打亂,每次隨機抽取一個球記錄顏色,並將該球和一個額外的,與該球相同顏色的球放入罈子。不斷重複上述操作,則對任意類型為的球,其被抽取的機率有如下表示:
式中
表示抽得c類小球的機率,
表示第c類球在罈子中的個數。定義所有顏色小球在第m次抽取中被抽到的機率為隨機變數
,則當抽取次數趨於無窮時,隨機變數服從特定的狄利克雷分布:
推廣
其它機率分布
對服從狄利克雷分布的隨機變數
,定義新的隨機變數
,則該隨機變數服從逆狄利克雷分布(inverted Dirichlet distribution)。狄利克雷分布和逆狄利克雷分布都是多元劉維爾分布(multivariate Liouville distribution)的特例。
當狄利克雷分布的先驗與
多項分布的似然的乘積對模型參數取邊緣分布時,可以得到狄利克雷-多項分布(Dirichlet-multinomial distribution)。狄利克雷-多項分布也被稱為
波利亞分布(Pólya distribution),是一類在有限空間取值的混合分布(mixture distribution),在
貝葉斯推斷(Bayesian inference)中有套用,也是Beta-二項分布(beta-binomial distribution)在高維情形的推廣。此外以狄利克雷分布為基礎可以得到廣義狄利克雷分布(generalized Dirichlet distribution)和組合狄利克雷分布(Grouped Dirichlet distribution),其中前者在狄利克雷分布中引入額外的分布參數,被用於處理有缺失的類型數據(incomplete categorical data),而後者是狄利克雷分布在多個類型變數(categorical variable)下的推廣。
狄利克雷過程(Dirichlet Process, DP)
DP是狄利克雷分布由機率分布向
隨機過程(stochastic process)的推廣,即給定一參數空間,若其有狄利克雷分布的基分布(base distribution),且該參數空間的任意有限劃分的測度(邊緣分布)都是狄利克雷分布,則所有劃分得到的分布的集合是DP,基分布為DP的數學期望。狄利克雷分布與DP的關係可以類比
常態分配與
高斯過程(Gaussian process)的關係。DP作為狄利克雷分布的推廣,在非參數貝葉斯推斷(nonparametric Bayesian inference)中有套用,常見的例子是DP混合模型(DP mixture model)。
套用
在
貝葉斯推斷中,狄利克雷分布作為多項分布的共軛先驗,被用於
多項分布、
二項分布和類型分布(categorical distribution)的參數估計。在
機器學習領域,狄利克雷分布和廣義狄利克雷分布被套用於構建
混合模型(mixture model)以處理高維的聚類和特徵賦權(feature weighting)等
非監督學習問題。使用狄利克雷分布建立的
主題模型(topic model),即
隱含狄利克雷分布(Latent Dirichlet Allocation, LDA)被套用於
自然語言處理(Natural Language Processing, NLP)和
生物信息學研究(bioinfomatics)。

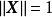
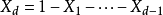
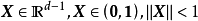

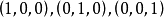

 3維對稱狄利克雷分布,左至右:稀疏分布,均勻分布,密集分布
3維對稱狄利克雷分布,左至右:稀疏分布,均勻分布,密集分布