相對熵(relative entropy),又被稱為Kullback-Leibler散度(Kullback-Leibler divergence)或信息散度(information divergence),是兩個機率分布(probability distribution)間差異的非對稱性度量。在在信息理論中,相對熵等價於兩個機率分布的信息熵(Shannon entropy)的差值。
相對熵是一些最佳化算法,例如最大期望算法(Expectation-Maximization algorithm, EM)的損失函式。此時參與計算的一個機率分布為真實分布,另一個為理論(擬合)分布,相對熵表示使用理論分布擬合真實分布時產生的信息損耗。
基本介紹
- 中文名:相對熵
- 外文名:relative entropy
- 別名:Kullback-Leibler散度,信息散度
- 提出者:S. Kullback,R. A. Leibler
- 提出時間:1951年
- 學科:統計學,信息科學
- 套用:信息分析,機器學習
理論,性質,套用,
理論
定義
設 是隨機變數
是隨機變數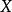 上的兩個機率分布,則在離散和連續隨機變數的情形下,相對熵的定義分別為:
上的兩個機率分布,則在離散和連續隨機變數的情形下,相對熵的定義分別為:


推導
在信息理論中,相對熵是用來度量使用基於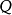 的編碼來編碼來自
的編碼來編碼來自 的樣本平均所需的額外的比特個數。典型情況下,
的樣本平均所需的額外的比特個數。典型情況下, 表示數據的真實分布,
表示數據的真實分布,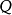 表示數據的理論分布,模型分布,或
表示數據的理論分布,模型分布,或 的近似分布。給定一個字元集的機率分布,我們可以設計一種編碼,使得表示該字元集組成的字元串平均需要的比特數最少。假設這個字元集是
的近似分布。給定一個字元集的機率分布,我們可以設計一種編碼,使得表示該字元集組成的字元串平均需要的比特數最少。假設這個字元集是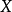 ,對
,對 ,其出現機率為
,其出現機率為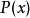 ,那么其最優編碼平均需要的比特數等於這個字元集的熵:
,那么其最優編碼平均需要的比特數等於這個字元集的熵:
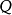


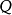

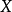

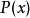

在同樣的字元集上,假設存在另一個機率分布 ,如果用機率分布
,如果用機率分布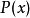 的最優編碼(即字元
的最優編碼(即字元 的編碼長度等於
的編碼長度等於 ),來為符合分布
),來為符合分布 的字元編碼,那么表示這些字元就會比理想情況多用一些比特數。相對熵就是用來衡量這種情況下平均每個字元多用的比特數,因此可以用來衡量兩個分布的距離,即:
的字元編碼,那么表示這些字元就會比理想情況多用一些比特數。相對熵就是用來衡量這種情況下平均每個字元多用的比特數,因此可以用來衡量兩個分布的距離,即:

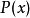




計算實例
這裡給出一個對相對熵進行計算的具體例子。假如一個字元發射器,隨機發出0和1兩種字元,真實發出機率分布為A,但實際不知道A的具體分布。通過觀察,得到機率分布B與C,各個分布的具體情況如下:

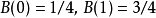
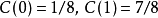





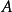
吉布斯不等式(Gibbs inequality)
由於對數函式是凸函式(convex function),所以根據相對熵的定義有: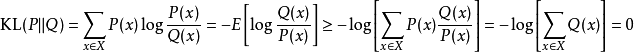 由上式可知,相對熵始恆大於等於0的。若且唯若兩分布相同時,相對熵等於0。
由上式可知,相對熵始恆大於等於0的。若且唯若兩分布相同時,相對熵等於0。
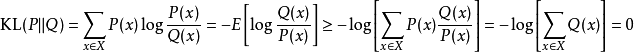
性質
非負性:由吉布斯不等式可知,相對熵恆為非負: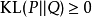 ,且在
,且在 時取0。
時取0。
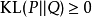

不對稱性:相對熵是兩個機率分布的不對稱性度量,即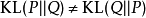 。在最佳化問題中,若
。在最佳化問題中,若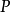 表示隨機變數的真實分布,
表示隨機變數的真實分布, 表示理論或擬合分布,則
表示理論或擬合分布,則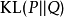 被稱為前向KL散度(forward KL divergence),
被稱為前向KL散度(forward KL divergence), 被稱為後項KL散度(backward KL divergence)。前向散度中擬合分布是KL散度公式的分母,因此若在隨機變數的某個取值範圍中,擬合分布的取值趨於0,則此時KL散度的取值趨於無窮。因此使用前向KL散度最小化擬合分布和真實分布的距離時,擬合分布趨向於覆蓋理論分布的所有範圍。前向KL散度的上述性質被稱為“0避免(zero avoiding)”。相反地,當使用後向KL散度求解擬合分布時,由於擬合分布是分子,其0值不影響KL散度的積分,反而是有利的,因此後項KL散度是“0趨近(zero forcing)”的。
被稱為後項KL散度(backward KL divergence)。前向散度中擬合分布是KL散度公式的分母,因此若在隨機變數的某個取值範圍中,擬合分布的取值趨於0,則此時KL散度的取值趨於無窮。因此使用前向KL散度最小化擬合分布和真實分布的距離時,擬合分布趨向於覆蓋理論分布的所有範圍。前向KL散度的上述性質被稱為“0避免(zero avoiding)”。相反地,當使用後向KL散度求解擬合分布時,由於擬合分布是分子,其0值不影響KL散度的積分,反而是有利的,因此後項KL散度是“0趨近(zero forcing)”的。
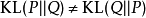
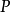

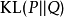

與信息理論中其它概念的關係:對前向KL散度,其值等於真實分布與擬合分布的交叉熵與真實分布的信息熵之差:

套用
相對熵可以衡量兩個隨機分布之間的距離,當兩個隨機分布相同時,它們的相對熵為零,當兩個隨機分布的差別增大時,它們的相對熵也會增大。所以相對熵可以用於比較文本的相似度,先統計出詞的頻率,然後計算相對熵。另外,在多指標系統評估中,指標權重分配是一個重點和難點,也通過相對熵可以處理。