簡介 不定方程(indeterminate equation)是
數論 的一個
分支 ,它有著
悠久 的
歷史 與豐富的內容。所謂不定方程是指解的範圍為
整數 、
正整數 、有理數或
代數整數 的方程或方程組,其未知數的個數通常多於方程的個數。
古希臘數學家
丟番圖 於三世紀初就研究過若干這類
方程 ,所以不定方程又稱
丟番圖方程 ,是數論的重要分支學科,也是歷史上最活躍的數學領域之一。不定方程的內容十分豐富,與
代數數論 、
幾何數論 、集合數論等等都有較為密切的聯繫。1969年,
莫德爾 較系統地總結了這方面的研究成果。
圖1 不定方程淺說 歷史 古希臘的
丟番圖 早在公元3世紀就開始研究不定方程,因此常稱不定方程為
丟番圖方程 。
Diophantus ,古代希臘人,被譽為
代數學 的鼻祖,流傳下來關於他的生平事跡並不多。今天我們稱整
係數 的不定方程為「Diophantus方程」,內容主要是探討其整數解或有理數解。他有三本著作,其中最有名的是《
算術 》,當中包含了189個問題及其答案,而許多都是不定
方程組 (變數的個數大於方程的個數)或
不定方程式 (兩個變數以上)。丟番圖只考慮
正有理數 解,而不定方程
通常 有無窮多解的。
圖2 丟番圖 研究不定
方程 要解決三個問題:①判斷何時有解。②有解時決定解的個數。③求出所有的解。中國是研究不定方程最早的國家,公元初的
五家共井 問題就是一個不定
方程組 問題,公元5世紀的《
張丘建算經 》中的
百雞問題 標誌中國對不定方程理論有了系統研究。
秦九韶 的
大衍求一術 將不定方程與
同餘 理論聯繫起來。百雞問題說:“雞翁一,直錢五,雞母一,直錢三,雞雛三,直錢一。百錢買百雞,問雞翁、母、雛各幾何?”。設x,y,z分別表雞翁、母、雛的個數,則此問題即為不定方程組的
非負整數 解x,y,z,這是一個三元不定方程組問題。
圖3 數書九章——大衍類 常見類型 ⑴求不定方程的整數解;
⑵判定不定方程是否有解;
⑶判定不定方程的解的個數(有限個還是無限個)。
一次不定方程 二元一次不定方程的一般形式為ax+by=c。其中 a,b,c 是整數,ab ≠ 0。此方程有整數解的
充分必要條件 是a、b的最大
公約數 整除c。設
、
是該方程的一組整數解,那么該方程的所有整數解可表示為
.
S(≥2)元一次不定方程的一般形式為
,
為整數,且
。此方程有整數解的充分必要條件是
的
最大公約數 整除n。
埃拉托塞尼 篩法產生的
素數 普遍公式是一次不定方程 公元前300年,古希臘數學家
歐幾里得 就發現了數論的本質是素數,他自己證明了有無窮多個素數,公元前250年古希臘數學家埃拉托塞尼發明了一種篩法:
一,“要得到不大於某個自然數N的所有素數,只要在2~N中將不大於
的素數的倍數全部划去即可”。
二,後來人們將上面的內容等價轉換:“如果N是合數,則它有一個因子d滿足1<d≤
”。(《基礎數論》13頁,U杜德利著,上海科技出版社)..
三,再將二的內容等價轉換:“若自然數N不能被不大於
的任何素數整除,則N是一個素數”。見(代數學辭典[上海教育出版社]1985年。屜部貞世朗編。259頁)。
四,上面這句話的漢字可以等價轉換成為用英文字母表達的公式:
。
⑴ 其中
表示順序素數2,3,5...。a≠0。即N不能是2m+0,3m+0,5m+0,...,
形。若N<
的平方,則N是一個素數。
五可以把(1)等價轉換成為用同餘式組表示:
N≡
(mod
), N≡
(mod
),.....,N≡
(mod
)。⑵
例如,29,29不能夠被
以下的任何素數2,3,5整除,29=2x14+1=3x9+2=5x5+4。29≡1(mod2),29≡2(mod3), 29≡4(mod5)。29小於7的平方49,所以29是一個素數。
由於⑵的模p1,p2,....,pk 兩兩互素,根據
孫子定理 (中國剩餘定理)知,⑵在
範圍內有唯一解。例如k=1時,N=2m+1,解得N=3,5,7。求得了(3,3^2)區間的全部素數。k=2時,N=2m+1=3m+1,解得N=7,13,19; N=2m+1=3m+2,解得N=5,11,17,23,求得了(5,5*)區間的全部素數。
k=3時,
---------------------| 5m+1-|- 5m+2-| 5m+3,| 5m+4.|
---------------------|---------|----------|--------|---------|
n=2m+1=3m+1= |--31----|--7,37-|-13,43|--19----|
n=2m+1=3m+2= |-11,41-|-17,47-|--23---|---29---|
------------------------------------------------------------
求得了(7,7^2)區間的全部素數。仿此下去可以求得任意大的數以內的全部素數。
多元一次 關於整數多元一次不定方程,可以有
矩陣 解法、程式設計等相關方法輔助求解。
二次 二元二次不定方程本質上可以歸結為求二次曲線(即
圓錐曲線 )的
有理點 或整點問題。
一類特殊的二次不定方程是
,其正整數解稱商高數或
勾股數 或
畢達哥拉斯 數,中國《
周髀算經 》中有“勾廣三,股修四,經隅五”之說,已經知道 (3,4,5)是一個解。
劉徽 在注《
九章算術 》中又給出了(5,12,13),(8,15,17), (7,24,25),(20,21,29)幾組勾股數。它的全部正整數解已在16世紀前得到。這類方程本質上就是求橢圓上的有理點。
另一類特殊的二次不定方程是所謂
佩爾方程 ,D是非平方的正整數。利用
連分數 理論知此方程永遠有解。這類方程就是求
雙曲線 上的有理點。
最後一類就是平方剩餘問題, 即求
的整數解, 用
高斯 的
同餘 理論來描述,就是求
的
剩餘類 解。高斯發現的著名
二次互反律 給出了次方程是否有解的判定方法。這類方程就相當於求
拋物線 上的整點。圓錐曲線對應的不定方程求解可以看做橢圓曲線算術性質的一種特例。
高次 對高於二次的不定方程,相當複雜。當n>2時,
沒有非平凡的整數解 ,即著名的費馬大定理,歷經3個世紀 ,已由英國數學家安德魯 ·維爾斯證明完全可以成立。
多元高次不定方程
多元高次不定方程沒有一般的解法,任何一種解法都只能解決一些特殊的不定方程,如利用二次域來討論一些特殊的不定方程的整數解。常用的解法:
⑴代數恆等變形:如因式分解、配方、換元等;
⑵不等式估算法:利用不等式等方法,確定出方程中某些變數的範圍,進而求解;
⑶同餘法:對等式兩邊取特殊的模(如奇偶分析),縮小變數的範圍或性質,得出不定方程的整數解或判定其無解;
⑷構造法:構造出符合要求的特解,或構造一個求解的遞推式,證明方程有無窮多解;
⑸無窮遞推法。
特殊方法 二元一次方程 定義1. 形如 ax + by = c ( a,b,c∈Z,a,b不同時為零)的方程稱為二元一次不定方程。
定理1. 方程 ax + by = c 有解的充要是 ( a,b ) | c;
定理2. 若(a,b)= 1,且
為 ax + by = c 的一個解,則方程的一切解都可以表示成
定理3. n元一次不定方程
有解的充要條件是:
.
方法與技巧:
1.解二元一次不定方程通常先判定方程有無解。若有解,可先求 ax + by = c 一個特解,從而寫出通解。當不定方程係數不大時,有時可以通過觀察法求得其解,即引入變數,逐漸減小係數,直到容易得其特解為止;
2.解n元一次不定方程
時,可先順次求出
. 若c不能被
整除,則方程無解;若c可以被
整除,則方程有解,作方程組:
求出最後一個方程的一切解,然後把
的每一個值代入倒數第二個方程,求出它的一切解,這樣下去即可得方程的一切解。
3.m個n元一次不定方程組成的方程組,其中 m < n,可以消去 m-1 個未知數,從而消去了 m-1 個不定方程,將方程組轉化為一個 n-m+1 元的一次不定方程。
高次方程 1.因式分解法:對方程的一邊進行因式分解,另一邊作質因式分解,然後對比兩邊,轉而求解若干個方程組;
2.同餘法:如果不定方程
有整數解,則對於任意 m∈N,其整數解
滿足
,利用這一條件,同餘可以作為探究不定方程整數解的一塊試金石;
3.不等式估計法:利用不等式工具確定不定方程中某些字母的範圍,再分別求解;
4.無限遞降法:若關於正整數n的命題 P(n) 對某些正整數成立,設
是使 P(n) 成立的最小正整數,可以推出:存在正整數n,使得
成立,適合證明不定方程無正整數解。
方法與技巧:
1.因式分解法是不定方程中最基本的方法,其理論基礎是整數的唯一分解定理,分解法作為解題的一種手段,沒有因定的程式可循,應具體的例子中才能有深刻地體會;
2.同餘法主要用於證明方程無解或導出有解的必要條件,為進一步求解或求證作準備。同餘的關鍵是選擇適當的模,它需要經過多次嘗試;
3.不等式估計法主要針對方程有整數解,則必然有
實數 解,當方程的實數解為一個有界集,則著眼於一個有限範圍內的整數解至多有有限個,逐一檢驗,求出全部解;若方程的實數解是無界的,則著眼於整數,利用整數的各種性質產生適用的不等式;
4.無限遞降法論證的核心是設法構造出方程的新解,使得它比已選擇的解“嚴格地小”,由此產生矛盾。
特殊的方程 1.利用分解法求不定方程 ax + by = cxy ( abc≠0 )整數解的基本思路:
將 ax + by = cxy 轉化為 (x - a)(cy -b) = ab 後,若 ab 可分解為
,則解的一般形式為
再取捨得其整數解;
2.定義2:形如的
的方程叫做勾股數方程,這裡x,y,z為正整數。
對於方程
,如果 (x,y) = d,則
,從而只需討論 (x,y) = 1 的情形,此時易知x,y,z兩兩互素,這種兩兩互素的正整數組叫方程的本原解。
定理3.勾股數方程滿足條件 2|y 的一切解可表示為:
其中 a > b > 0,(a,b) = 1, 且a,b為一奇一偶。
推論:勾股數方程的全部正整數解(x,y的順序不加區別)可表示為:
其中 a > b > 0 是互質的奇偶性不同的一對正整數,d是一個整數。勾股數不定方程的整數解的問題主要依據定理來解決。
3.定義3.方程
( x,y∈Z,正整數d不是平方數) 是
的一種特殊情況,稱為沛爾(Pell)方程。
這種
二元二次方程 比較複雜,它們本質上歸結為雙曲線方程
的研究,其中c,d都是整數,d > 0 且非平方數,而 c ≠ 0。它主要用於證明問題有無數多個整數解。對於具體的d可用嘗試法求出一組成
正整數 解。如果上述pell方程有正整數解(x,y),則稱使
的最小的正整數解為它的最小解。
定理4.Pell方程
( x,y∈Z,正整數d不是平方數)必有正整數解,且若設它的最小解為
,則它的全部解可以表示成:
上面的公式也可以寫成以下幾種形式:
定理5.Pell方程
( x,y∈Z,正整數d不是平方數)要么無正整數解,要么有無窮多組正整數解,且在後一種情況下,設它的最小解為
,則它的全部解可以表示為
|定理6. (
費爾馬 (Fermat)大定理)方程
(n≥3且為整數)無正整數解。
費爾馬(Fermat)大定理的證明一直以來是數學界的難題,但是在1994年6月,
美國普林斯頓大學 的數學教授A.Wiles完全解決了這一難題。至此,這一困擾了人們四百多年的
數學難題 終於露出了廬山真面目,脫去了其神秘面紗。
簡單例題 求11x+15y=7的整數解。
解法1 將方程變形得11x=7-15y
因為x是整數,所以7-15y應是11的倍數。由觀察得x=2,y=-1是這個方程的一組整數解,所以方程的解為x=2,y=-1。
解法2 先考察11x+15y=1,通過觀察易得11×(-4)+15×(3)=1,所以11×(-4×7)+15×(3×7)=7,可取x=-28,y=21。從而可見,二元一次不定方程在無約束條件的情況下,通常有無數組整數解,由於求出的特解不同,同一個不定方程的解的形式可以不同,但它們所包含的全部解是一樣的。將解中的參數t做適當代換,就可化為同一形式。
代數幾何 對於
多項式 不定方程, 我們相當於求解某個
代數簇 上的有理點或整點等等。這樣, 一個數論問題就轉化為某種幾何問題。這種觀點將數論與
代數幾何 聯繫起來,是一種重要的
數學思想 。對於
代數曲線 來說, 相應的不定方程是否有解的以及是否有無限個解, 都與曲線的
虧格 密切相關。這就是著名的莫代爾猜想(由
法爾廷斯 證明)所包含的內容。
虧格零的曲線就是直線和二次曲線, 他們就對應了上述的一次和二次不定方程。虧格1的是橢圓曲線, 它的算術性質和代數幾何性質極為豐富。它將數論、
複分析 、代數幾何、
表示論 等等都聯繫起來, 是當代數學最重要的研究對象之一。與此相關的是千禧年七大數學難題之一的BSD猜想。
著名的費馬大定理的證明也與此相關。
進展 這個領域更有重要進展。但從整體上來說,對於高於二次的多元不定方程,人們知道得不多。另一方面,不定方程與數學的其他分支如
代數數論 、
代數幾何 、
組合數學 等有著緊密的聯繫,在有限群論和最優設計中也常常提出不定方程的問題,這就使得不定方程這一古老的分支繼續吸引著許多數學家的注意,成為數論中重要的研究課題之一。
不定方程
費爾馬(Pierre de Fermat,1601~1665)法國著名數學家,被譽為“
業餘數學家 之王”。——費爾馬一生從未受過專門的數學教育,數學研究也不過是業餘之愛好。然而,在17世紀的法國還找不到哪位數學家可以與之匹敵:他是解析幾何的發明者之一;對於
微積分 誕生的貢獻僅次於艾薩克.牛頓、戈特弗里德.威廉.凡.萊布尼茨;又是機率論的主要創始人;還是獨承17世紀數論天地的人。此外,費爾馬對物理學也有重要貢獻。一代數學天才費爾馬堪稱是17世紀法國最偉大的數學家之一。
費爾馬的家庭非常富裕,因而接受了很好、很廣博的教育。當時還有“買官”的風氣,所以費爾馬得以一生都做官,而且官越當越大。
費爾馬雖然一直做著官,但對他來說,真正的事業是學術,尤其是數學。他通曉法語、義大利語、西班牙語、
拉丁語和希臘語 ,而且還頗有研究。語言方面的博學給他的數學研究提供了語言工具和便利,使他有能力學習和了解阿拉伯和義大利的
代數 以及古希臘的數學。正是這些,可能為費爾馬在數學上的造詣奠定了良好基礎。在數學上,費爾馬不僅可以在數學王國里自由馳騁,而且還可以站在數學天地之外鳥瞰數學。這也不能絕對歸於他的數學天賦,與他的博學多才多少也是有關係的。
費爾馬生性內向,謙抑好靜,不善推銷自己,不善展示自我。因此他生前極少發表自己的論著,連一部完整的著作也沒有出版。他發表的一些文章,也總是隱姓埋名。反映其成就的《數學論集》,還是費爾馬去世後由其長子將其筆記、批註及書信整理後編輯出版的。多虧了這個好兒子啊!如果不是他積極出版其父的數學論著,那很難說費爾馬能對數學產生那么重大的影響,並被譽為“業餘數學家之王”。
費爾馬的貢獻很多,但最出名的要數其中的“費爾馬大定理”。這是一個與“
哥德巴赫猜想 ”一類的
數學難題 ,下面就說說它。
費爾馬大定理的內容:
當整數n > 2時,關於x,y,z的不定方
(n表示“n次方”)無正整數解。
1637年,費爾馬在閱讀丟番圖《算術》拉丁文譯本時,曾在第11卷第8命題旁寫道:“將一個立方數分成兩個立方數之和,或一個四次冪分成兩個四次冪之和,或者一般地將一個高於二次的冪分成兩個同次冪之和,這是不可能的。關於此,我確信已發現了一種美妙的證法 ,可惜這裡空白的地方太小,寫不下。”(拉丁文原文: "Cuius rei demonstrationem mirabilem sane detexi. Hanc marginis exiguitas non caperet.")畢竟費爾馬沒有寫下證明,而他的其它猜想對數學貢獻良多,由此激發了許多數學家對這一猜想的興趣。
1908年,德國佛爾夫斯克宣布以10萬馬克作為獎金獎給在他逝世後一百年內,第一個證明該定理的人。當時吸引了不少人嘗試並遞交他們的“證明”,但都沒成功。
最後,在1995年,亦即(從問題提出到解決)經過了三個半世紀的努力後,這道世紀數論難題才由
普林斯頓大學 英國數學家——安德魯.懷爾斯和他的學生理查?泰勒成功證明。證明利用了很多新的數學,包括代數幾何中的橢圓曲線和模形式,以及
伽羅華 理論和Hecke代數等,這令人懷疑費爾馬當年是否真的找到了正確證明。
安德魯?懷爾斯(Andrew Wiles)由於成功證明此定理,獲得了1998年的
菲爾茲獎 特別獎以及2005年度
邵逸夫獎 的數學獎。當然他也拿到了那筆10萬馬克的獎金,因為還在規定的“破解期限”內。
而懷爾斯證明費爾馬大定理的過程亦甚具戲劇性。他用了7年時間,在不為人知的情況下,得出了證明的大部分;然後於1993年6月在一個學術會議上宣布了他的證明,並瞬即成為世界頭條。但在審批證明的過程中,專家發現了一個極嚴重的錯誤。懷爾斯和泰勒然後又用了近一年的時間嘗試補救,終在1994年9月以一個之前懷爾斯拋棄過的方法得到成功,他們的證明刊在1995年的數學年刊(en:Annals of Mathematics)之上。
 圖1 不定方程淺說
圖1 不定方程淺說 圖2 丟番圖
圖2 丟番圖 圖3 數書九章——大衍類
圖3 數書九章——大衍類


























































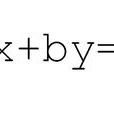
 圖1 不定方程淺說
圖1 不定方程淺說 圖2 丟番圖
圖2 丟番圖 圖3 數書九章——大衍類
圖3 數書九章——大衍類


























































