基本介紹
- 中文名:一元二次方程
- 外文名:quadratic equation of one unknown
- 類型:整式方程
- 標準形式:ax2+bx+c=0(a≠0)
- 求根公式:x=[-b±√(b2-4ac)]/2a
- 學科領域:數學、代數
發展歷史,成立條件,主要形式,一般形式,變形式,配方式,兩根式,方程的解,含義及特點,判別式,韋達定理,求解方法,開平方法,配方法,求根公式,因式分解,圖像解法,計算機法,
發展歷史
公元前2000年左右,古巴比倫的數學家就能解一元二次方程了。他們是這樣描述的:已知一個數與它的倒數之和等於一個已知數,求出這個數。他們使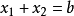
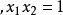
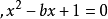 再做出解答。可見,古巴比倫人已知道一元二次方程的解法,但他們當時並不接受負數,所以負根是略而不提的。古埃及的紙草文書中也涉及到最簡單的二次方程,例如:
再做出解答。可見,古巴比倫人已知道一元二次方程的解法,但他們當時並不接受負數,所以負根是略而不提的。古埃及的紙草文書中也涉及到最簡單的二次方程,例如: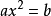 。
。
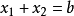
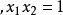
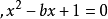
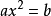
公元前300年左右,古希臘的歐幾里得(Euclid)(約前330年~前275年)提出了用一種更抽象的幾何方法求解二次方程。古希臘的丟番圖(Diophantus)(246~330)在解一元二次方程的過程中,卻只取二次方程的一個正根,即使遇到兩個都是正根的情況,他亦只取其中之一。
公元628年,印度的婆羅摩笈多(Brahmagupta)(約598~約660)出版了《婆羅摩修正體系》,得到了一元二次方程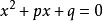 的一個求根公式。
的一個求根公式。
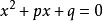
公元820年,阿拉伯的阿爾·花剌子模(al-Khwārizmi)(780~810)出版了《代數學》。書中討論到方程的解法,除了給出二次方程的幾種特殊解法外,還第一次給出了一元二次方程的一般解法,承認方程有兩個根,並有無理根存在,但卻未有虛根的認識。他把方程的未知數叫做“根”,後被譯成拉丁文(radix)。其中涉及到六種不同的形式,令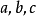 為正數,如
為正數,如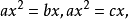
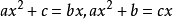 等。把二次方程分成不同形式作討論,是依照丟番圖的做法。
等。把二次方程分成不同形式作討論,是依照丟番圖的做法。
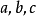
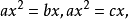
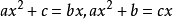
法國的韋達(1540~1603)除推出一元方程在複數範圍內恆有解外,還給出了根與係數的關係。
成立條件
一元二次方程成立必須同時滿足三個條件:
②只含有一個未知數;
③未知數項的最高次數是2。
主要形式
一般形式
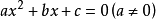
使方程左右兩邊相等的未知數的值就是這個一元二次方程的解,一元二次方程的解也叫做一元二次方程的根。
變形式
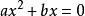
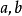
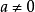
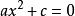
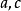
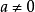

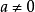
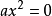
配方式
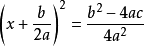
兩根式
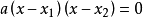
方程的解
含義及特點
(1)一元二次方程的解(根)的意義:能使一元二次方程左右兩邊相等的未知數的值稱為一元二次方程的解。一般情況下,一元二次方程的解也稱為一元二次方程的根(只含有一個未知數的方程的解也叫做這個方程的根)。
(2)由代數基本定理,一元二次方程有且僅有兩個根(重根按重數計算),根的情況由判別式(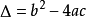 )決定。
)決定。
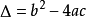
判別式
利用一元二次方程根的判別式(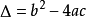 )可以判斷方程的根的情況。
)可以判斷方程的根的情況。
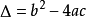
①當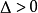 時,方程有兩個不相等的實數根;
時,方程有兩個不相等的實數根;
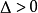
②當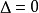 時,方程有兩個相等的實數根;
時,方程有兩個相等的實數根;
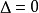
③當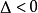 時,方程無實數根,但有2個共軛復根。
時,方程無實數根,但有2個共軛復根。
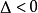
上述結論反過來也成立。
韋達定理
設一元二次方程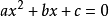
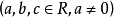 中,兩根
中,兩根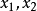 有如下關係 :
有如下關係 :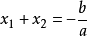
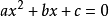
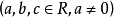
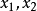
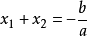
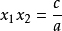
這一定理的數學推導如下:
由一元二次方程求根公式知
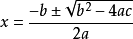
則有:
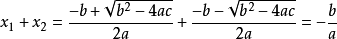

求解方法
開平方法
(2)如果方程化成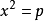 的形式,那么可得
的形式,那么可得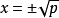 。
。
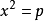
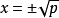
(3)如果方程能化成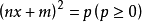 的形式,那么
的形式,那么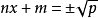 ,進而得出方程的根。
,進而得出方程的根。
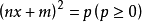
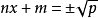
(4)注意:
①等號左邊是一個數的平方的形式而等號右邊是一個常數。
②降次的實質是由一個一元二次方程轉化為兩個一元一次方程。
③方法是根據平方根的意義開平方。
配方法
將一元二次方程配成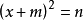 的形式,再利用直接開平方法求解的方法。
的形式,再利用直接開平方法求解的方法。 圖1配方法解一元二次方程實例
圖1配方法解一元二次方程實例
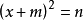
 圖1配方法解一元二次方程實例
圖1配方法解一元二次方程實例(1)用配方法解一元二次方程的步驟:
①把原方程化為一般形式;
②方程兩邊同除以二次項係數,使二次項係數為1,並把常數項移到方程右邊;
③方程兩邊同時加上一次項係數一半的平方;
④把左邊配成一個完全平方式,右邊化為一個常數;
⑤進一步通過直接開平方法求出方程的解,如果右邊是非負數,則方程有兩個實根;如果右邊是一個負數,則方程有一對共軛虛根。
(2)配方法的理論依據是完全平方公式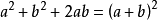
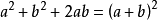
(3)配方法的關鍵是:先將一元二次方程的二次項係數化為1,然後在方程兩邊同時加上一次項係數一半的平方。
求根公式
(1)用求根公式法解一元二次方程的一般步驟為: 圖 求根公式推導
圖 求根公式推導
 圖 求根公式推導
圖 求根公式推導①把方程化成一般形式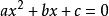 ,確定
,確定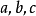 的值(注意符號);
的值(注意符號);
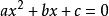
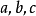
②求出判別式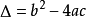 的值,判斷根的情況;
的值,判斷根的情況;
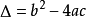
③在 (註:此處△讀“德爾塔”)的前提下,把
(註:此處△讀“德爾塔”)的前提下,把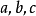 的值代入公式
的值代入公式 進行計算,求出方程的根。
進行計算,求出方程的根。

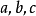

(2)推導過程
一元二次方程的推導如右圖2。
注意:一元二次方程的求根公式在方程的係數為有理數、實數、複數或是任意數域中適用。一元二次方程中的判別式: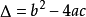 ,應該理解為“如果存在的話,兩個自乘後為的數當中任何一個”。在某些數域中,有些數值沒有平方根。
,應該理解為“如果存在的話,兩個自乘後為的數當中任何一個”。在某些數域中,有些數值沒有平方根。
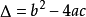
因式分解
因式分解法即利用因式分解求出方程的解的方法。 圖3因式分解法舉例
圖3因式分解法舉例
 圖3因式分解法舉例
圖3因式分解法舉例因式分解法解一元二次方程的一般步驟如下:
①移項,使方程的右邊化為零;
②將方程的左邊轉化為兩個一元一次方程的乘積;
③令每個因式分別為零
④括弧中 ,它們的解就都是原方程的解。
,它們的解就都是原方程的解。

圖像解法
當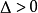 時,則該函式與
時,則該函式與 軸相交(有兩個交點);
軸相交(有兩個交點);
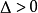

當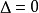 時,則該函式與
時,則該函式與 軸相切(有且僅有一個交點);
軸相切(有且僅有一個交點);
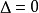

當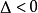 時,則該函式與軸
時,則該函式與軸 相離(沒有交點)。
相離(沒有交點)。
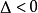

(2)另外一種解法是把一元二次方程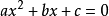 化為:
化為: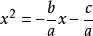 的形式。則方程的根,就是函式
的形式。則方程的根,就是函式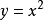 和
和 交點的
交點的 坐標。通過作圖,可以得到一元二次方程根的近似值。
坐標。通過作圖,可以得到一元二次方程根的近似值。
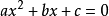
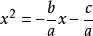
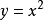


計算機法
在使用計算機解一元二次方程時,和人手工計算類似,大部分情況下也是根據求根公式來求解,即:
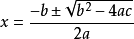
可以進行符號運算的程式,如軟體Mathematica,可以給出根的解析表達式,而大部分程式則只會給出數值解(但亦有部分顯示平方根及虛數的情況)。

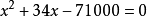
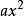


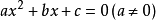
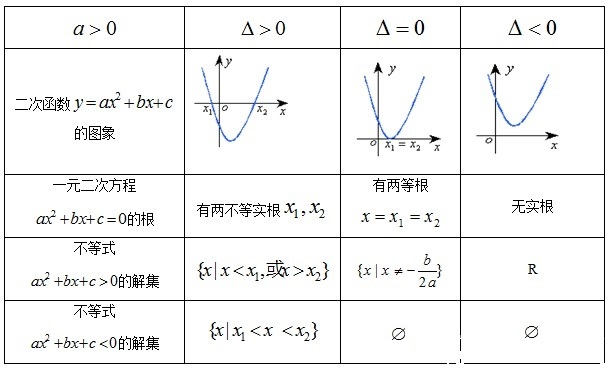 圖4圖像法解方程
圖4圖像法解方程