基本介紹
定義
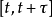

- 在一個時間區間或空間區域內的事件數,和另一個互斥(不重疊)的時間區間或空間區域內的事件數,這兩個隨機變數是獨立的。
泊松簡介
 法國著名數學家泊松
法國著名數學家泊松性質
- Tn(n=1,2,...)是獨立同分布的指數隨機變數,具有均值1/λ。
名詞解釋
推廣
 非齊次泊松過程
非齊次泊松過程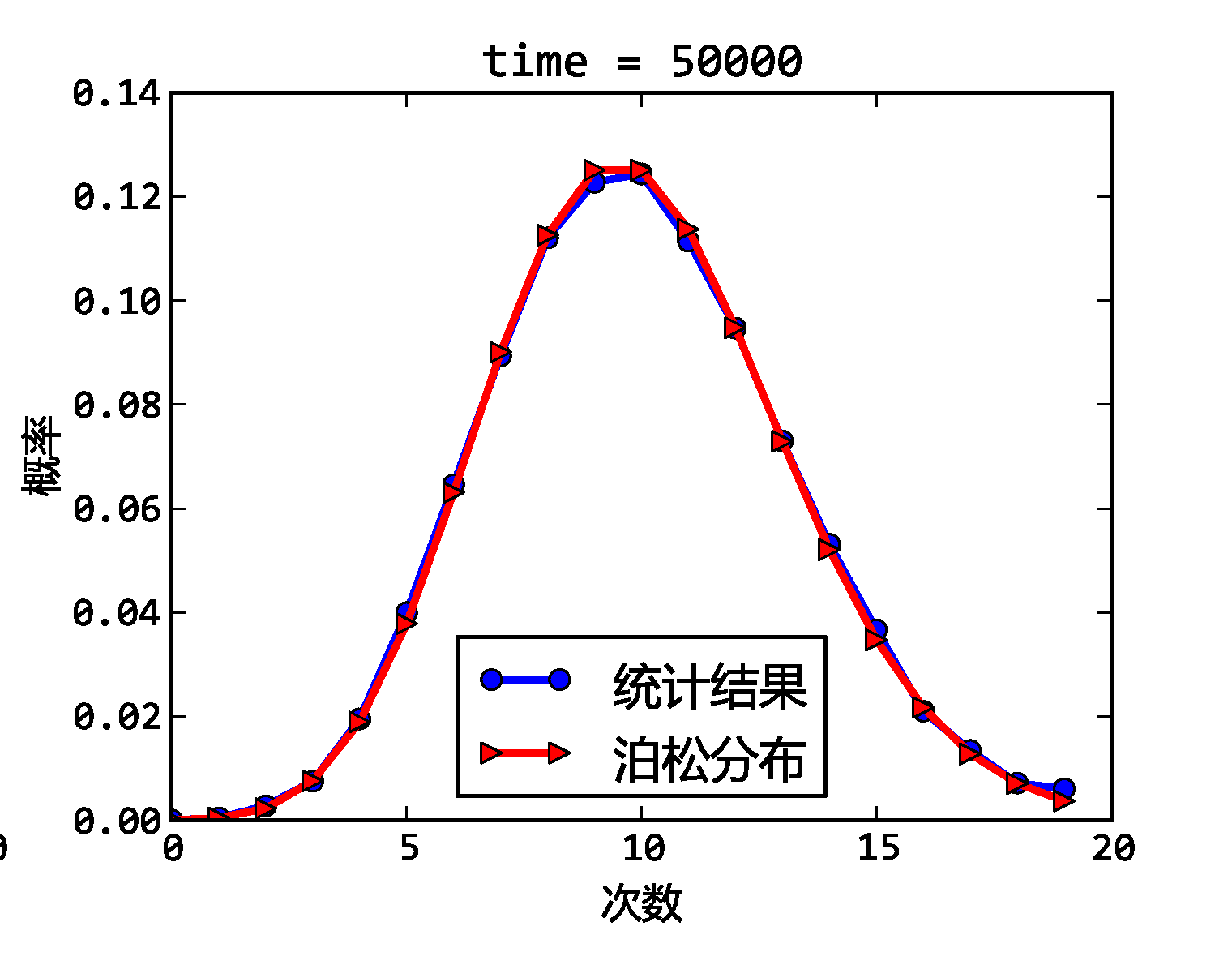
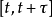

 法國著名數學家泊松
法國著名數學家泊松 非齊次泊松過程
非齊次泊松過程一種累計隨機事件發生次數的最基本的獨立增量過程。例如隨著時間增長累計某電話交換台收到的呼喚次數,就構成一個泊松過程。 泊松過程是由法國著名數學家泊松(Poisson,...
齊次泊松過程(homogeneous Poisson process )是一類既簡單又在理論和套用中起著重要作用的隨機點過程。...
Poisson分布,是一種統計與機率學裡常見到的離散機率分布,由法國數學家西莫恩·德尼·泊松(Siméon-Denis Poisson)在1838年時發表。...
《泊松點過程》是2013年科學出版社出版的一本圖書,作者是Roy L. Streit。...... 《泊松點過程:成像、跟蹤和感知》提出了一種學習泊松點過程(PPP)的結構性方法,...
重隨機泊松過程(doubly stochastic Poissonprocess)亦稱柯克斯過程一類隨機點過程。是柯克斯於1955年在研究處於隨機環境的泊松過程時引入的。這類過程可以看做是點發生...
複合泊松過程,高等數學模型。複合泊松過程可以看做是在泊松過程的點附上標值(用隨機變數Y,表示)而得。複合泊松過程(compound Poisson process)一類隨機過程.是由對...
西莫恩·德尼·泊松(Simeon-Denis Poisson 1781~1840)法國數學家、幾何學家和物理學家。1781年6月21日生於法國盧瓦雷省的皮蒂維耶,1840年4月25日卒於法國索...
濾過泊松過程(filtered Poisson process)一類隨機過程.是對泊松過程施行某種變換即“濾過”而產生的隨機過程.對隨機過程{X(t>,t妻。},如果它能表為 其中{N(t...
廣義齊次泊松過程(generalized homogeneousPoisson process)亦稱平穩無後效流一種齊次泊松過程.在齊次泊松過程的定義中除去有序性條件就得到廣義齊次泊松過程。可以證明,...
非齊次泊松過程(non-homogeneous Poisson process)【1】是泊松過程一個推廣.如果允許泊松過程的定義中時刻t的來到強度(或速率)是t的函式λ(t),就得到非齊次泊松...
簡稱重泊松分布。 ...... 簡稱重泊松分布。 [1] 參考資料 1. 鄭家亨,統計大辭典,中國統計出版社,1995年03月第1版,第90頁 V百科往期回顧 詞條統計 瀏覽次數...
馬爾可夫過程(Markov process)是一類隨機過程。它的原始模型馬爾可夫鏈,由俄國數學家A.A.馬爾可夫於1907年提出。馬爾可夫過程是研究離散事件動態系統狀態空間的重要方法...
《泊松點過程——成像、跟蹤和感知》是一本科學出版社2013年出版的圖書,作者是〔美〕斯特利特(Streit,R.L.)。...
泊松回歸(英語:Poisson regression)是用來為計數資料和列聯表建模的一種回歸分析。泊松回歸假設反應變數Y是泊松分布,並假設它期望值的對數可被未知參數的線性組合建模...
泊松定理為一定理,由法國力學家、物理學家和數學家S.D.泊松總結出。從泊松定理出發進行公式推導和分析,闡述了重磁異常的對應分析3個參數的物理意義,並認為在區域...
在機率論中,聯合泊松分布也稱複合泊松分布,是指一些獨立同分布的隨機變數的和的機率分布,而這些隨機變數的個數服從。在最簡單的情形下,聯合泊松分布可以是連續分布...
混合泊松過程(mixed Poisson process)一種泊松過程,指強度本身是一個隨機變數的泊松過程,它既可以看做是泊松過程的推廣。...
描述隨機點分布的隨機過程。很多隨機現象發生的時刻、地點、狀態等往往可以用某一空間上的點來表示。例如,服務台前顧客的到來時刻,真空管陰極電子的發射時刻,可表為...
輸入過程是排隊論的基本概念之一,指顧客到達排隊系統的過程(情況)。顧客總體(稱為顧客源)可能是有限的,也可能是無限的;顧客到來的方式可能是單個的,也可能是成...
