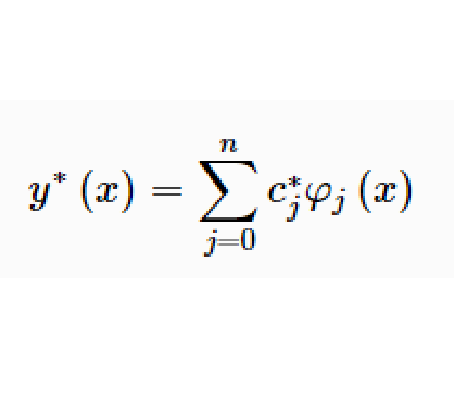擬合曲線

在工程設計或科學實驗中所得到的數據往往是一張關於離散數據點的表 ，沒有解析式來描述 x-y關係。根據所給定的這些離散數據點繪製的曲線，稱為不規則曲線，通常用曲線擬合的方法解決這類問題。所謂曲線擬合方法是由給定的離散數據點，建立數據關係(數學模型)，求出一系列微小的直線段把這些插值點連線成曲線，只要插值點的間隔選擇得當，就可以形成一條光滑的曲線。曲線一般有兩類：規則曲線和自由曲線。規則曲線都可以用函式或參數方程來表示，而擬合曲線是對離散點進行插值、逼近繪製的。

基本介紹

• 中文名：擬合曲線
• 外文名：fitted curve
• 所屬學科：數理科學
• 概要：對離散點進行插值、逼近繪製
• 擬合曲線類型：指數函式、冪函式、雙曲線擬合等

基礎介紹

對於平面上給定的點 ，要尋找y與x之間的近似函式關係 ，插值法要求曲線 準確通過每個給定點 ；而m較大時無論是高次插值還是分段低次插值都將很複雜，數據 一般是由實驗觀測得到的，總會帶有觀測誤差，刻意要求 並不能反映真實的函式關係，反而會引起 的波動加劇，因此用 近似描述已知數據 ，不必要求在每個點處，誤差 ，都為0，只需在所有點處的某種總體誤差最小即可，這就是所謂的曲線擬合問題，亦稱為離散函式最佳平方逼近問題。

設給定基函式 ，我們在集合

中尋求形如 的函式，使其近似已知數據。

定義1 對給定的數據 ，若

使得

則稱 為曲線族中的最小二乘擬合曲線，並稱

為均方誤差。

要確定擬合曲線(1)中的待定係數 ，由(2)式知，就是求多元函式

的最小值點()，由多元函式取極值的必要條件，有

從而有

這是n+1個方程、n+1個未知數的線性方程組，藉助矩陣運算，可寫成如下矩陣形式：

其中， 而

方程組(3)稱為法方程組，設 線性無關(且滿足Haar條件)，則行列式 ，線性方程組(3)存在唯一的一組解。

若取基函式 ，法方程的係數矩陣顯然非奇異，此時一般稱為多項式擬合，求解法方程組，得到擬合係數

從而得到

再由多元函式取極值的充分條件可證明，這樣求出的 確實是方程組(2)的解，即 為最小二乘擬合曲線。

幾種具體的擬合曲線類型

以上討論的都是線性最小二乘擬合問題，即擬合曲線 ，也就是 是基函式 的線性組合，有些問題雖然數學模型不是線性模型，但通過變換可化為線性模型，則上述最小二乘擬合方法仍然可用。

指數函式擬合

選取擬合函式為指數函式

為待定常數，

這是一個關於 的非線性模型，現通過適當變換將其化為線性模型，為此對 兩邊取對數，有

令於是

這是一個關於 的線性模型，原來的已知數據 經取對數後變成一組新數據 ，這裡

對這組新數據，求形如 的擬合曲線。

取基函式 則由(3)式可得法方程組，求解出 後即得到擬合曲線 ，從而得到

冪函式擬合

選取擬合函式為冪函式

為待定常數，

這也是關於 的非線性模型．兩邊取對數，同樣可將其化為線性模型，即

令 則擬合曲線為

這時基函式為將原數據中的取對數，得新數據其中對此新數據，用擬合即可。

雙曲型擬合

雙曲型 也是關於 的非線性擬合模型，作變形

令 ，則擬合曲線為化成了關於 的線性擬合模型，這時新數據為 ，其中 。基函式為由法方程組(3)即可求出擬合曲線進而求出擬合曲線。