基本介紹
概論,歷史,數學定義,性質,
概論
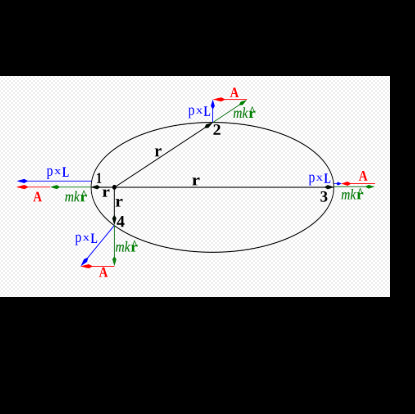
在一個物理系統里,在任意保守的有心力的作用下,一個粒子的運動,都會擁有至少四個運動常數;能量與角動量L的三個分量皆為運動常數。粒子的軌道被限制於一個平面。粒子的動量P和從力中心點的位置到粒子位置的位移r。粒子的運動平面垂直於角動量L。用方程表示,

歷史
在重要的克卜勒問題中,LRL矢量A是一個運動常數,時常用來描述天文軌道,例如行星的運動。然而,物理學家對它並不熟悉,這很可能是因為與動量與角動量相比,它的物理內涵比較難以被直覺地理解。因此,在過去三個世紀裡,它曾被重複地發現過許多次。1710年,在一個不著名的義大利學刊里,雅各布·赫爾曼最先發表了關於LRL矢量的論文。在推導一個軌道方程的過程中,他計算出LRL矢量的大小,A是保守的;並且推導出此案例與橢圓軌道離心率的關係。稍後,赫爾曼把這結果告訴約翰·伯努利,他的恩師。伯努利又更進一步地推導出LRL矢量的方向。這樣,LRL矢量得到了它的現代形式。所以,不容質疑地,LRL矢量是赫爾曼和伯努利共同發現的。
在那個世紀末尾,皮埃爾-西蒙·拉普拉斯又重新地發現了LRL矢量的保守性;稍微不同地,他的導引使用的是分析方法,而不是幾何方法。十九世紀中葉,威廉·哈密頓推導出全等的離心率矢量。他用離心率矢量來證明,在平方反比有心力作用下,速端曲線顯示出,粒子動量矢量的頭部呈圓形移動(參閱圖3)。二十世紀初,約西亞·吉布斯,套用矢量分析,推導出同樣的矢量。後來,卡爾·龍格將吉布斯的導引,納入自己所寫的一本廣受歡迎的,關於矢量的,德文教科書內,成為其中的一個例題。1924年,威爾漢·楞次發表了一篇關於氫原子的舊量子論的論文。在這篇論文中,他引用龍格所寫的教科書的例題為參考。1926年,沃爾夫岡·泡利用LRL矢量與矩陣力學,而不是薛丁格方程,來推導氫原子的光譜。這傑作說服了大多數物理學家,使他們覺得量子力學理論是正確的。
數學定義

感受到此力的作用,一個粒子的軌道運動,其LRL矢量的數學定義方程為


這個單獨粒子的LRL矢量定義,也可以延伸至像克卜勒問題一類的二體問題,只需要設定質量m為二個物體的約化質量,設定位置矢量r為二個物體之間的相對位置矢量。
同樣的運動常數可以有很多種不同的表述.最常見的一種牽涉到離心率矢量。定義離心率矢量e為LRL矢量與mk的除商:

性質
在克卜勒問題里,LRL矢量的保守性對應於系統的一種微妙的對稱性。在經典力學里,對稱性可以由連續運算顯示出來;這連續運算可以將一個軌道映射至另外一個軌道,而同時保持系統的能量不變。在量子力學里,連續運算將同能級原子軌域混合在一起,也就是說,(簡併原子能級)。
通常,對於每一個對稱性都會存在有一個保守量。例如,有心力系統必對稱於旋轉群SO(3);因而指引出角動量L的保守性。在經典力學里,整個系統的旋轉不會影響軌道的能量。在量子力學里,假若旋轉只混合角量子數相同的球諧函式,則系統的能量不會改變。
平方反比有心力系統的對稱性是更高維與更微妙的。這奇特的對稱性是由角動量L與LRL矢量A的雙重保守性造成的;這保證了氫原子的能級跟角量子數I、磁量子數m無關。由於對稱性運算必須發生於更高維空間,使得這對稱性更加的微妙;這類的對稱性常稱為隱秘對稱性。在經典力學裡,克卜勒問題的高維對稱性容許連續的改變軌道.只要保持能量不變,而角動量可以改變;換句話說,同能量,不同角動量(離心率)的軌道可以互相的連續變換。在量子力學裡,這對應著不同角量子數與磁量子數的軌域的混合,例如s(l=0)與p(l=1)原子軌域的混合。這種混合是不能用普通的三維平移運算或旋轉運算達成的。可是,這種混合等價於高維度空間的旋轉。
在一個束縛(bounded)系統里,能量是負值的,這高維對稱群是SO(4);特性是四維矢量的長度保持不變:

1935年,弗拉基米爾·佛克(Vladimir Fock)表明,在量子力學裡,束縛的克卜勒問題等價於一個粒子自由地移動於四維空間的三維單位球。更具體地,佛克表明,在克卜勒問題的動量空間,薛丁格波函式是球諧函式的球極平面投影。圓球的旋轉與重複射影造成了橢圓軌域的連續映射,同時維持能量不變;這對應於主量子數n相同的軌域的混合。隨後,華倫泰·巴格曼注意到,跟LRL矢量成比例的矢量D與角動量L的泊松括弧形成SO(4)的李代數。簡單地說,D與L的六個物理量對應於在四維空間裡的六個保守的角動量分量,相伴於在四維空間裡的六個合法的簡單旋轉(從四個軸中,選兩個軸為旋轉軸。一共有六種可能)。這結論並不意示宇宙是一個三維球面;而只是說,這個特別的物理問題(克卜勒問題),在數學上,等價於移動於三維球面的一個自由粒子。