基本介紹
- 中文名:泊松括弧
- 外文名:Poisson bracket
- 套用範圍:數學及經典力學
- 提出者:泊松
- 實質:是哈密頓力學重要的運算
- 相關名詞:泊松定理
簡介
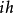
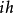
定義
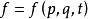

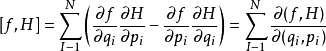
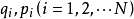
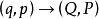
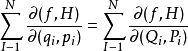


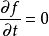
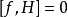
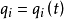


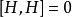

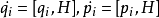
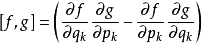
性質
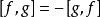
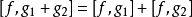
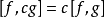
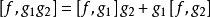
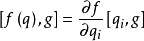
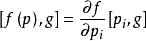
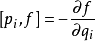
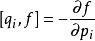
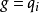
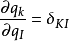
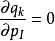
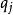
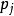
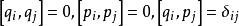
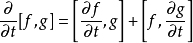

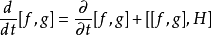

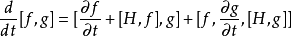
在量子力學中
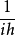
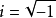
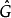
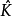

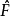

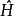
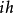
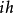
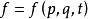

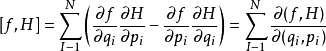
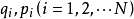
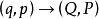
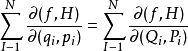


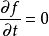
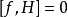
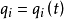


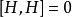

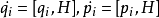
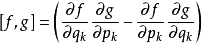
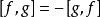
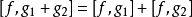
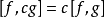
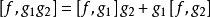
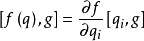
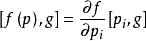
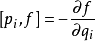
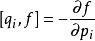
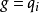
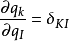
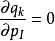
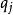
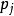
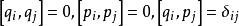
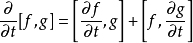

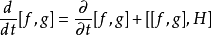

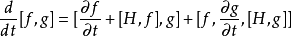
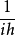
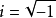
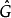
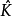

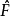

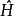
泊松括弧在數學及經典力學中是哈密頓力學重要的運算,在哈密頓表述的動力系統中時間推移的定義起著中心角色。泊松括弧在量子力學中有很重要的作用。它與量子力學的...
量子泊松括弧,又稱對易子,是一種雙線性的運算,類似於李代數。由於量子力學中的對易子運算與理論力學中的泊松括弧有對應關係,故而也稱量子泊松括弧。...
西莫恩·德尼·泊松(Simeon-Denis Poisson 1781~1840)法國數學家、幾何學家和物理學家。1781年6月21日生於法國盧瓦雷省的皮蒂維耶,1840年4月25日卒於法國索...
拉格朗日括弧法國數學家和力學家 J.-L.拉格朗日研究正則變換時所用的一種數學符號。拉格朗日括弧是一種與泊松括弧關係密切的運算,1808年至1810年間由約瑟夫·拉格朗日...
在微分幾何中,斯豪滕–奈恩黑斯括弧(Schouten–Nijenhuis bracket,國際音標:[ˈsχʌutən]-[ˈnɛiənhœys]),也稱為斯豪滕括弧。...
埃倫費斯特定理與哈密頓力學的劉維爾定理密切相關;劉維爾定理使用的泊松括弧,對應於埃倫費斯特定理的對易算符。實際上,從根據經驗法則,將對易算符換為泊松括弧乘以 ,...
多體問題或其他動力系統的首次積分組成的一個特殊系統,其中任意兩個組合的泊松括弧恆等於零。對合系統性質 編輯 按照李氏(Lie , M. S.)定理,若有 k 個首次...
全書分7章,主要內容包括:分析力學形成前夕和初期的動力學方程及方法;拉格朗日動力學;多自由度力學體系的微振動;哈密頓動力學;正則變換;泊松括弧與拉格朗日括弧;哈密...
對應於流形上的函式 f 與g 的兩個哈密頓向量場的李括弧也是一個哈密頓向量場,其哈密頓函式由 g 與f 的泊松括弧給出。中文名 哈密頓向量場 外文名 ...
典則變換(canonical transformation)餘切叢 上保持泊松括弧不變的微分同胚.設:是從餘切叢 T幾)到餘切叢T . }'}y)上的微分同胚.在局 部坐標下,:表示變換y-y...
