單調有界定理：單調有界數列必收斂（有極限）。
基本介紹
- 中文名：單調有界定理
- 外文名：The monotone bounded convergence theorem
- 數學範疇：數學分析-純數學
- 數學理論：極限理論
- 誕生源：微積分
- 意義：給出了數列極限的判定定理
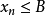
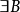
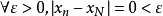
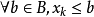
相關概念,單調性,有界性,定理,證明,套用,注意事項,
相關概念
單調性
對任一數列{xn}，如果從某一項xk開始，滿足
則稱數列（從第k項開始）是單調遞增的。特別地，如果上式全部取小於號，則稱數列是嚴格單調遞增的。
同樣地，如果從某一項k開始，滿足
則稱數列（從第k項開始）是單調遞減的。特別地，如果上式全部取大於號，則稱數列是嚴格單調遞減的。
單調遞增數列和單調遞減數列統稱單調數列。
有界性
對任一數列{xn}，如果存在某個實數A使數列的所有項都滿足不等式
恆成立，即
，使得
恆成立，即
，使得
則稱這個數列是有上界的，實數B是數列的一個上界，記做
。
如果一個數列既有上界又有下界，則稱這個數列是有界的。此時，存在一個正數M，使不等式
定理
單調有界數列必有極限。具體地說：
（i）若數列
遞增且有上界，則
（ii）若數列 遞減且有下界，則
證明
設數列{xn}單調遞增且有上界，接下來用戴德金定理證明{xn}必有極限。
分類討論，如果{xn}從第N項開始所有的項都相等（即數列有無窮多個相等的項），那么由於數列是單調遞增的，當n>N時，有xn=xN，因此對
。即{xn}收斂到xN。
如果{xn}中只有有限項相等，即數列從某項開始嚴格單調遞增，那么因為{xn}有上界，可取所有{xn}的上界組成一個數集B，並取A=R/B。則：
①由取法可知數集B非空，而{xn}為嚴格單調遞增數列，故
。∴
。
②
。
③∵A中任何元素都不是{xn}的上界，∴
。
又∵B中任何元素都是{xn}的上界，∴
。
故必有
。
∴由戴德金定理可知，存在唯一實數η，使得η要么是A中的最大值，要么是B中的最小值。
但無論是哪種情況，
。
④由數集A的意義可知，
。而數列單調遞增，故當
時，
。
⑤由數集B的意義可知，當 時，
。
綜合④⑤可知，當 時，
∴
，即{xn}有極限。
同理可證：若數列{xn}單調遞減且有下界，則{xn}必有極限。
套用
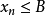
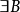
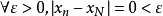
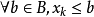
在一般的教科書中，單調有界定理是通過確界原理來證明的，即通過確界原理知道{xn}有上（下）確界α，再證明{xn}收斂於α。事實上，單調有界定理與確界原理等價，既可以由確界原理得到單調有界定理，也可以由單調有界定理得到確界原理。以下是其證法。
問題：試通過單調有界定理證明確界原理。
解：不妨設數集S非空有上界，將所有不小於S中的任一元素的有理數排成一個數列{rn}，並令{xn}=min{r1,r2,r3...rn}。為更直觀理解{xn}，舉例如下：
設S=[1,2]。第一次，取r1=3，則x1=min{3}=3。第二次，取r2=5，則x2=min{3,5}=3。第三次，取r3=2.5，則x3=min{3,5,2.5}=2.5。第四次，取r4=2.2，則x4=min{3,5,2.5,2.2}=2.2……以此類推。顯然{xn}單調遞減並且有下界（S中任何元素都是{xn}的下界），因此{xn}收斂。設極限為η，並且由上述構造可知，η≤xn≤rn。
利用反證法，
①若η不是S的上界，即存在p∈S，使p>η。取
，根據極限的幾何意義，存在正整數N，使不等式η<xN<η+ε成立。而
，從而xN<p。這與xN不小於S中的任一元素矛盾。
②任取a>0，若對任意k∈S，都有k≤η-a，根據有理數的稠密性（即任何兩個不相等的實數之間必定存在有理數），存在有理數r，使不等式k≤η-a<r<η成立。因為我們把所有不小於S中的任一元素的有理數排成了一個數列{rn}，r∈{rn}。這樣一來，就得到η≤r，矛盾。
所以，η是S的上確界。
注意事項
（1）單調有界定理只能用於證明數列極限的存在性，如何求極限需用其他方法；
（2）數列從某一項開始單調有界的話，結論依然成立，這是因為增加或去掉數列有限項不改變數列的極限。
