數列的極限問題是我們學習的一個比較重要的部分,同時,極限的理論也是高等數學的基礎之一。數列極限的問題作為微積分的基礎概念,其建立與產生對微積分的理論有著重要的意義。
基本介紹
- 中文名:數列極限
- 外文名:The limit of sequence
- 領域:數學
- 性質:數列的收斂性
- 套用:微積分
基本概念
數列
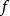
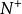

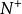
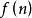


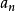
數列極限


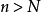




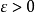


幾何意義
 圖1
圖1性質



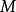
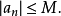
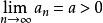
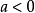
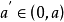
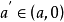
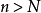
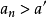
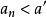

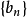

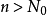
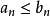
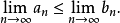

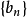
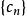
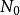


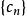
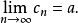

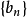
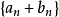
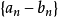
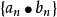
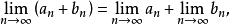
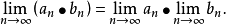
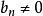
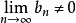
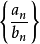
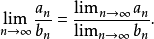
存在的條件
套用
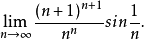
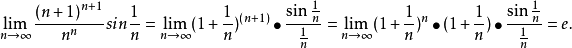

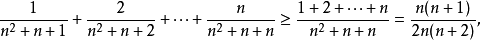
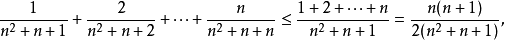
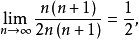
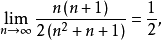
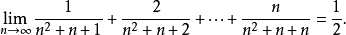
數列的極限問題是我們學習的一個比較重要的部分,同時,極限的理論也是高等數學的基礎之一。數列極限的問題作為微積分的基礎概念,其建立與產生對微積分的理論有著重要的意義。
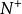

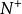
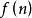


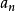


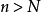




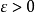


 圖1
圖1


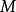
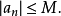
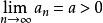
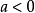
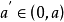
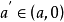
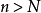
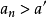
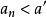

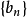

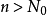
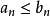
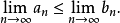

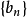
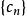
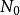


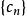
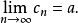

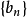
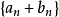
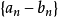
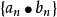
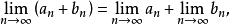
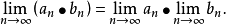
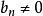
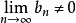
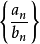
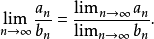
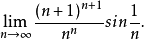
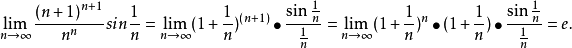

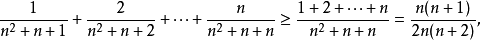
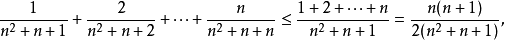
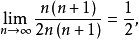
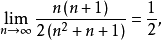
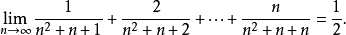
數列的極限問題是我們學習的一個比較重要的部分,同時,極限的理論也是高等數學的基礎之一。數列極限的問題作為微積分的基礎概念,其建立與產生對微積分的理論有著重要...
《數學專題研究數列極限數學歸納法》是2001年8月中國青年出版社出版的圖書,作者是王海平。...
極限理論是研究關於極限的嚴格定義、基本性質和判別準則等問題的基礎理論。極限思想的萌芽可以追溯到古希臘時期和中國戰國時期,但極限概念真正意義上的首次出現於沃利斯...
《超越吉米多維奇數列的極限》是2009年11月哈爾濱工業大學出版社出版的圖書,作者是《超越吉米多維奇:數列的極限》編寫組。...
函式極限是高等數學最基本的概念之一,導數等概念都是在函式極限的定義上完成的。函式極限性質的合理運用。常用的函式極限的性質有函式極限的唯一性、局部有界性、保...
極限,是指無限趨近於一個固定的數值。在高等數學中,極限是一個重要的概念:極限可分為數列極限和函式極限。...
上極限是指收斂子數列的極限值的上確界值。...... 上極限數列上極限 給定無窮數列 ,它的一切收斂子數列的極限值的上確界值,稱為該無窮序列的上極限。...
極限函式是高等數學中最基本的概念之一,它是判定函式列一致收斂的一個重要條件...... 函數列極限的 定義是:對每一固定的 ,任給正數 ,恆存在正數 (注意:一般說...
遞歸數列 (recursive sequence ):一種給定A1後,用給定遞歸公式An+1=f(An)由前項定義後項所得到的數列。...
數學術語,表示極限(limit)。極限是微積分中的基礎概念,它指的是變數在一定的變化過程中,從總的來說逐漸穩定的這樣一種變化趨勢以及所趨向的值(極限值)。...
夾逼定理英文原名Squeeze Theorem。也稱兩邊夾定理、夾逼準則、夾擠定理、挾擠定理、三明治定理,是判定極限存在的兩個準則之一。...
海涅定理是溝通數列極限與函式極限的橋樑。...... 海涅定理是溝通函式極限和數列極限之間的橋樑。根據海涅定理,求函式極限則可化為求數列極限,同樣求數列極限也可轉化...
O'Stolz定理是處理數列不定式極限的有力工具,一般用於*/∞型的極限(即分母趨於正無窮大的分式極限,分子趨不趨於無窮大無所謂)、0/0型極限(此時要求分子分母都以...
在高等數學中,極限是一個重要的概念。極限可分為數列極限和函式極限,分別定義如下。數列極限:[1] 數列極限1(2張) 函式極限:[1] 函式極限(2張) ...
