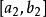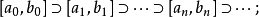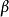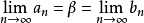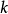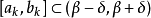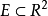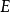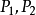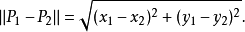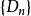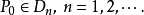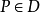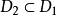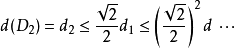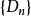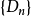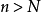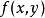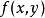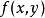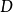函式是描述客觀世界變化規律的重要數學模型，連續函式又是數學分析中非常重要的一類函式。在數學中，連續是函式的一種屬性。而在直觀上來說，連續的函式就是當輸入值的變化足夠小的時候，輸出的變化也會隨之足夠小的函式。函式極限的存在性、可微性，以及中值定理、積分等問題，都是與函式的連續性有著一定聯繫的，而閉區間上連續函式的性質也顯得非常重要。在閉區間上連續函式的性質中，有界性定理又是最值定理和介值定理等的基礎。
基本介紹
- 中文名：有界性定理
- 外文名：boundedness theorem
- 套用學科：數學
- 適用領域範圍：數學分析
- 屬性：閉區間上的連續函式的性質
閉區間上的一元連續函式的有界性定理,定理1（一元連續函式的有界性定理）,定理2,閉域上二元連續函式的有界性定理,定義1,定理3（閉域套定理）,定理4（二元連續函式的有界性定理）,
在極限理論中，我們知道閉區間上連續函式具有5個性質，即：有界性定理、最大值與最小值定理、介值定理、零點定理和一致連續性定理。其中，零點定理是介值定理的一個重要推論。而閉區間上連續函式的有界性定理的證明，在很多數學教材中，有多種方法可以證明此定理。比如可以利用閉區間套定理、確界定理、單調有界定理和柯西收斂準等。我們知道，分析數學上所列舉的實數完備性的7個基本定理是相互等價的，因而從原則上講，任何一個都可以證明該定理。在本文中，我們分別討論一元連續函式和二元連續函式的有界性定理，分別給出一種證明方法。
閉區間上的一元連續函式的有界性定理
定理1（一元連續函式的有界性定理）
若函式f在閉區間
上連續，則f在 上有界。
證 套用區間套定理。假設函式f在閉區間
上無界。將區間 二等分，函式f必在
或
上無界，將函式f在其上無界的閉子區間記為
。如果函式f在這兩個閉區間上都無界，則任取其一記為 。
同理，將區間 二等分，則函式f必在其中一個閉子區間上無界，將其記為
。用二等分方法無限次地進行下去，構造出閉區間列
，滿足：
（i）
（ii）
①函式f在每個閉區間
上都無界。根據閉區間套定理，存在惟一的數
屬於所有的閉區間，且
②另一方面，已知
，則對上述
，必存在足夠大的
，使得
。因為函式f在區間
上無界，所以函式在區間 上無界。
①與②矛盾，假設不成立。於是函式f在區間
上有界。證畢。
根據有界性定理以及函式的連續性，我們可以得到下面的最大、最小值定理。
定理2
若函式f在閉區間
上連續，則f在上有最大值與最小值。
閉域上二元連續函式的有界性定理
定義1
設
，E是有界區域，正數
定理3（閉域套定理）
設
是
中的閉域列，它滿足：
（i）
（ii）
則存在惟一一點
定理4（二元連續函式的有界性定理）
若二元函式
在有界閉域
上連續，則函式在
上有界，即存在正數M，對於任意
，有
。
證 假設二元連續函式
在有界區域D上是無界的。設D的直徑為
，選取D的一條直徑，以該直徑為邊長，作一個正方形，使得D完全包含在該正方形中，然後分別連線該正方形兩組對邊的中點，則這兩條連線會將該正方形四等分，而有界閉域D會被分為有限個小區域。
由於在有界閉域D上無界，則至少存在某個小閉域，使在該小閉域上是無界的，記該小閉域為
，直徑為
，則
，且
。
重複上述過程，又可將有界閉域劃分為有限個小閉域，又至少存在某個小閉域，記為
，使在該閉域上無界。記的直徑為
，則
，且
。如此這般無限重複地做下去，即可得到一有界閉域列
。
該閉域列滿足：
（i）
（ii）
（iii）在每一個
上無界。
由（i），（ii）知
為一閉域套，由閉域套定理知，存在惟一一點
，且對任意
，存在
，當
時，
。
因為
，所以函式
在點
連續，根據連續函式的局部有界性可知存在
，使得在
內有界。
取上述的
，則存在
，當
時，
，從而在閉域
上有界，這與條件（iii）矛盾。
所以在閉域
上有界。證畢。
上述用閉域套定理對有界閉域上二元連續函式的有界性定理進行證明，從一側面反映了此證明與用閉區間套定理證明閉區間上連續函式的有界性定理有異曲同工之妙，但值得注意的是：利用閉區間套定理證明閉區間上連續函式的有界性定理時，只需要將該閉區間不斷地二等分，就可以得到一列閉區間套；利用閉域套定理對閉域上二元連續函式的有界性定理進行證明時，我們應該將該閉域幾等分，如何去等分卻是個難題。
