凸集分離定理是凸集理論的最基本的定理,它是指在很弱的條件下,兩個不相交的凸集總可用超平面分離。
基本介紹
- 中文名:凸集分離定理
- 外文名:Separating Hyperplane Theorem
- 別稱:超平面分離定理
- 套用學科:物理
- 兩個凸集分離:兩個凸集合沒有交叉和重合的部分
- 範數的等價性:這裡的範數可以是任何一種範數
定義
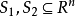




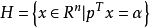

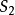
證明



引理


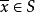
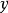

引理證明
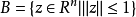
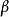



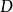

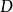





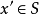
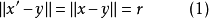
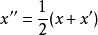





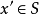
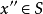



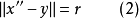

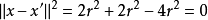

定理證明



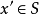







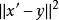

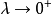



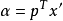
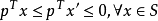
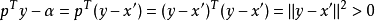

凸集分離定理是凸集理論的最基本的定理,它是指在很弱的條件下,兩個不相交的凸集總可用超平面分離。
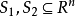




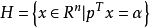







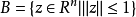
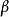



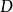

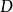





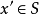
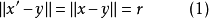
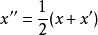





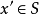
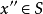



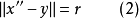

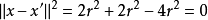




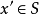







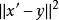

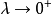



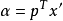
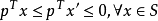
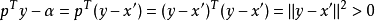

凸集分離定理是凸集理論的最基本的定理,它是指在很弱的條件下,兩個不相交的凸集總可用超平面分離。...
凸集支撐定理即相對代數內部非空的凸集的每一代數邊界點上都存在支撐該凸集的超平面。...
分離定理是關於公司投資決策可以與投資者個人偏好分離的經濟理論。公司的目標是價值最大化,與所有者的偏好無關。因此,管理者的投資決策應當與投資者的市場機會分離...
閔可夫斯基定理套用 編輯 閔可夫斯基定理是卡拉西奧多里定理對於緊凸集的精確化。在有些文獻中,也把凸集分離定理稱為閔可夫斯基定理。 [1] ...
哈恩一巴拿赫定理(Hahn-Banach theorem) [1] 線性函式的延拓定理.哈恩一巴拿赫定理是線性泛函分析的基本定理,但它實際上與凸集分離定理等價,因而也可看做凸集分離...
凸集理論在基礎數學、套用數學中都有十分重要的地位。作為前蘇聯學派代表性工作的端點定理(即Krein-Milman定理)是指局部凸線性拓撲空間中的每一緊凸集等於其端點的...
既是錐又是凸集的點集稱之為凸錐。常見的凸錐包括:二維平面中的半射線、整個n維歐式空間等。凸錐中有一個重要的定理,凸錐分離定理。...
凸集的交仍是凸集,如果C,D是R中的兩個凸集,則C+D={x+y|x∈C,y∈D}和λC={λx|x∈C}都是凸集。在數學規劃中,許多重要結果能夠利用凸集的分離定理來...
介紹最優解集的存在性定理、投影定理、凸集分離定理、極小公共點與極大交叉點對偶問題以及一般性的極小極大定理和鞍點定理;第3章討論凸集為多面體的情況,介紹線性...
本書作為一部數理經濟學專著,緊密貫穿最最佳化主題,從基礎的凸集、凸錐到凹函式...第三節 凸集的分離定理………/28第四節 分離定理在經濟學中的套用………...
代數閉包的概念在敘述凸集分離定理時也起重要作用。有的文獻定義代數閉包時,要求對於任何λ∈(0,ε)都有b+λh∈A。這時代數閉集就不再是代數開集的余集。但...
設A是拓撲線性空間X的子集,A相對其閉仿射包的內部稱為A的相對內部。這個概念在拓撲線性空間理論中不太用,但是在凸集分離定理的敘述中,它起重要作用 [1] 。...
利用凸集分離定理可以得到一系列有關芬切爾問題的解和拉格朗日乘子的存在定理。例如,如果f和g都是下半連續凸函式,且Y的原點為dom g-im A的內點(它在凸數學規劃...
它也是X在以代數開集為開集的拓撲意義下的閉集,即代數閉集的余集必定是代數開集;反之亦然.代數閉包的概念在敘述凸集分離定理時也起重要作用。有的文獻定義代數...
,那么根據凸集分離定理,即知存在一個閉超平面,亦即有界線性泛函 ,使得對於所有的p∈P,由於P是閉的,應有 。由於P是X中的凸錐,所以 ,所以特別有 ,此與命題之...
其主要目的在於利用集合和函式的凸性來處理各種分析問題,特別是極值問題,包括有限維的數學規劃問題和無限維的變分學問題.其主要工具是凸集分離定理、次微分理論和...
針對衛星儀器艙布局問題,套用集值映射與凸集分離定理等凸分析的基本理論,建立了具有多種性能約束的布局最佳化模型。依據圖論、對稱群對集合的作用、軌道及不可微最佳化...
(A),那么A稱為代數閉集.它也是X在以代數開集為開集的拓撲意義下的閉集,即代數閉集的余集必定是代數開集;反之亦然.代數閉包的概念在敘述凸集分離定理時也起...
紹凱積分表示理論(Choquet theory of integralrepresentation)是基於凸集和凸錐理論的積分表示理論。在緊凸集情形,紹凱積分表示定理是克列因-米爾曼定理的推廣。...
代數閉包的概念在敘述凸集分離定理時也起重要作用。有的文獻定義代數閉包時,要求對於任何λ∈(0,ε)都有b+λh∈A.這時代數閉集就不再是代數開集的余集。但當...
非空.相對代數內部的概念在凸集分離定理的敘述中也起重要作用.任何有限維空間中的凸集的相對代數內部總是非空的.而無限維空間中總存在相對代數內部為空的非空凸集...
5.5 資產定價基本定理的證明 5.6 凸集分離定理與資產定價基本定理 5.7 未定市場的一般經濟均衡和資產定價第二基本定理 5.8 說明資產定價基本定理的一個簡單例子 ...
第1章和第2章分別介紹凸集和凸函式的概念和有關性質;第3章引入凸函式的次微分,給出凸函式的極值條件與中值定理,並介紹次微分的性質和特殊凸函式的次微分表達式...
代數閉包的概念在敘述凸集分離定理時也起重要作用。有的文獻定義代數閉包時,要求對於任何λ∈(0,ε)都有b+λh∈A.這時代數閉集就不再是代數開集的余集。但當...
3.3.1凸集及凸集的分離定理 3.3.2凸集的Minkowski泛函,線性泛函的延拓 3.3.3局部凸空間 3.3.4弱拓撲,商拓撲 3.3.5弱*拓撲 3.3.6端點,Кре...
7.1.2 凸集分離定理及其套用7.1.3 凸函式與下半連續函式7.1.4 凸錐與對偶錐7.1.5 緊門集的端點表現7.2 泛函最最佳化問題與最優控制...
