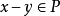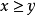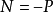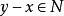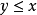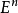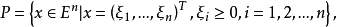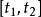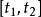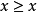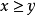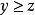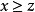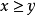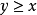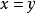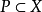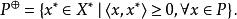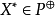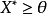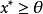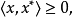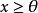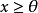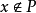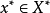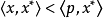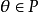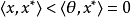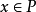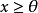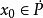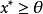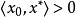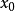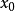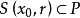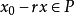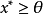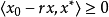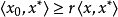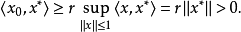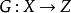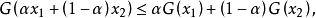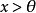正錐

正錐是偏序群的正元素集，若G是偏序群，則G的正元素集G⁺={g∈G|g>0}及G的負元素集G^-={g∈G|g<0}分別稱為G的正錐及負錐。G⁺滿足三個條件: 1.G⁺+G⁺⊆G⁺；2.G⁺∩-G+=G⁺∩G^-={0}；3.對任意a∈G有a+G⁺-a⊆G⁺。反之，若P是群G的子集，G的運算記為+，且P滿足條件1、2、3，對任意x，y∈G，定義x>y若且唯若x-y∈P，則由P可誘導出G的一個序，使G成為偏序群，且P=G⁺，於是，一個偏序群的序完全由滿足上述條件的子集P所確定，因此，亦稱P是G的一個序。

基本介紹

• 中文名：正錐
• 外文名：positive cone
• 所屬學科：數學
• 相關概念：偏序群、序關係、凸映射等

基本介紹

在給定的線性空間中，可以引進一個凸錐來規定一種序關係。這是討論線性空間中不等式關係的一個必不可少的前提。

定義 設X是一個線性空間，P足X中的一個凸錐，並且對於任意的 與 ，若 ，則記為 。對於這樣的P稱為X中的一個正凸錐，有時簡稱為正錐；若令 ，則稱N為X中的負凸錐，簡稱為負錐。顯然，若 ，則有 。

例如，在 中凸錐

它定義了Eⁿ中的正卦限；又例如，在區間 上所有函式構成的線性空間中，其凸錐自然可以定義為 上的所有非負函式構成的集合。

正錐與凸映射

很容易驗證，上述定義中的序關係，滿足以下三條性質：

1.自反性 。

2.傳遞性 若 ，又 ，則 。

3.對稱性 若 ，又 ，則 。

如果在X中定義了序關係“≥”，並且滿足上述三條公理，那么就稱在X中用正錐P定義了偏序關係。對於偏序關係我們需注意，在X中並非任意兩個元素都是可比的，所以才稱之為偏序。

在賦范線性空間中，有時用閉凸錐來定義正錐具有特殊的意義。另外，如果x是正錐P的一個內點，那么可以把它記為 。對於許多套用問題，為了能夠使用凸集分離定理，P至少要有一個內點，這是必不可少的條件。

給定一個賦范線性空間X與一個正凸錐 ，還可以在其對偶空間X*中定義一個對應的對偶正凸錐

對此， ，又可以記作 。

即使P不一定是閉的，而 卻總是閉的。如果P是閉的，那么在P與 之間有下列關係：

命題1 設X是一個賦范線性空間，P是X中的正凸錐，並且P是閉的。若x∈X，對於所有的 ，滿足 則 。

證明： 用反證法假設不成立，即，那么根據凸集分離定理，即知存在一個閉超平面，亦即有界線性泛函，使得對於所有的p∈P，由於P是閉的，應有。由於P是X中的凸錐，所以，所以特別有，此與命題之假設不符。故必有，即。

命題2 設X是一個賦范線性空間，P是X中的正凸錐，若 ，則對於所有非零的 ，有 。

證明:由於是P的內點，所以存在一個以為中心，以r>o為半徑的閉球，即當時，有。由於，所以，即。從而根據範數的定義，有

以上，我們已經推廣了向量不等式的概念，這就有可能使我們引進關於映射的凸性定義。

定義 設X是一個線性空間，Z也是一個線性空間，在Z中具有正凸錐P。若映射 ，G的定義域是Ω，Ω是X中的凸集，並且對於所有的x₁，x₂∈Ω以及α∈ [0，1]，有

則稱G是一個凸映射。