基本介紹
簡介
名稱定義


特徵介紹
分支
焦點
準線
離心率

頂點
實軸
虛軸
漸近線



頂點連線斜率

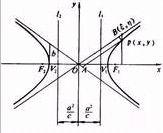 雙曲線
雙曲線實際套用
面積公式



重點
取值範圍
對稱性
頂點
漸近線


離心率
焦半徑
等軸雙曲線
共軛雙曲線
準線
光學性質
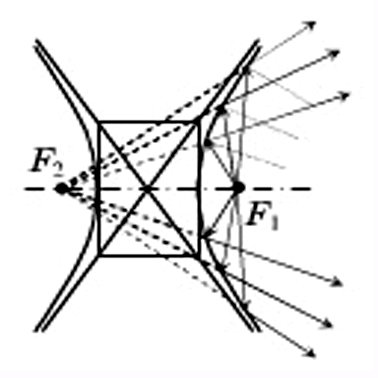 雙曲線的光學性質
雙曲線的光學性質







 雙曲線
雙曲線




 雙曲線的光學性質
雙曲線的光學性質一般的,雙曲線(希臘語“ὑπερβολή”,字面意思是“超過”或“超出”)是定義為平面交截直角圓錐面的兩半的一類圓錐曲線。它還可以定義為與兩個固定的...
雙曲線(Hyperbola)是指與平面上到兩個定點的距離之差的絕對值為定值的點的軌跡,也可以定義為到定點與定直線的距離之比是一個大於1的常數的點之軌跡。雙曲線是...
雙曲正切函式(hyperbolic tangent function)是雙曲函式的一種。雙曲正切函式在數學語言上一般寫作tanh,也可簡寫成th。與三角函式一樣,雙曲函式也分為雙曲正弦、雙...
正雙曲線是指漸近線互相垂直的雙曲線,即半長軸與半短軸相等。也稱直角雙曲線。...... 正雙曲線是指漸近線互相垂直的雙曲線,即半長軸與半短軸相等。也稱直角雙...
雙曲正弦函式是雙曲函式的一種。雙曲正弦函式在數學語言上一般記作sinh,也可簡寫成sh。與三角函式一樣,雙曲函式也分為雙曲正弦、雙曲餘弦、雙曲正切、雙曲...
漸近線定義為如果曲線上的一點沿著趨於無窮遠時,該點與某條直線的距離趨於零,則稱此條直線為曲線的漸近線。雙曲線漸近線方程,是一種幾何圖形的算法,這種主要解決...
圓錐曲線,是由一平面截二次錐面得到的曲線。圓錐曲線包括橢圓(圓為橢圓的特例)、拋物線、雙曲線。起源於2000多年前的古希臘數學家最先開始研究圓錐曲線。圓錐曲線(...
雙曲線定位(hyperbolic positioning)是通過測定待定點到至少三個已知點的兩個距離差所進行的一種無線電定位。定位參數是距離差,位置線是雙曲線。定位時需由至少三個...
實軸和虛軸等長的雙曲線叫做等邊雙曲線。此時,在雙曲線方程x^2/a^2-y^2/b^2=1中,a=b,於是得x^2-y^2=a^2。雙曲線的漸近線方程y=±(b/a)x變為y...
雙曲線的參數方程是以焦點(c,0)和(-c,0)為圓心,R為變半徑的曲線方程。...... 雙曲線的參數方程是以焦點(c,0)和(-c,0)為圓心,R為變半徑的曲線方程。...
雙曲線一號S火箭是北京星際榮耀空間科技有限公司研發的國內第一枚真正意義上的民營火箭,也是美國以外第一枚取得飛行成功的民營火箭。2018年4月5日2時00分,“雙...
王淵超於1995年讀高中時創作了這首歌曲。創作靈感來源於一堂解析幾何課,當時老師正在論證講解“雙曲線與漸近線只能無限接近不能達到”,而正是這點給王淵超帶來了創作...
雙曲線一號S火箭是北京星際榮耀空間科技有限公司研發的國內第一枚真正意義上的民營火箭,也是美國以外第一枚取得飛行成功的民營火箭。2018年4月5日2時00分,“雙...
“雙曲線一號(Hyperbola-1)”是星際榮耀研發的商業火箭,為四級固體小型運載火箭,箭體直徑為1.4m,全箭總長20m。2018年9月5日,商業亞軌道火箭雙曲線一號發射成功。...
與雙曲線虛軸相對應...... 與雙曲線虛軸相對應 雙曲線與坐標軸兩交點的連線段AB叫做實軸[1] 。實軸的長度為2a(a為標準方程中的參數)。...
在數學中,雙曲函式是一類與常見的三角函式(也叫圓函式)類似的函式。最基本的雙曲函式是雙曲正弦函式sinh和雙曲餘弦函式cosh,從它們可以導出雙曲正切函式tanh等,...
中變動時( 時定義G為三角形的重心, 時定義G為三角形的垂心),G點的軌跡為一條雙曲線,稱為三角形ABC的基佩特雙曲線。基佩特雙曲線性質 編輯 1:任意三角形的基佩...
雙曲線導航系統(hyperbolic navigation system)是利用雙曲線位置線實現導航定位的無線電導航系統。據解析幾何可知,距兩個固定點的距離差為常數的動點之軌跡,是以這兩...
雙曲線的殺人案 歲末年初的東京連續發生持槍搶劫案,嫌疑犯鎖定在一對雙胞胎兄弟的身上;然而兄弟二人巧妙地鑽了法律的空子,不僅持續作案而不被定罪,甚至輕而易舉地...
雙曲線型冷卻塔編輯 鎖定 hyperbolic cooling tower 火電廠、核電站的循環水自然通風冷卻塔是一種大型薄殼型構築物。建在水源不十分充足的地區的電廠,為了節約用水...
雙曲線函式 作者 徐玉相 類別 雙曲函式 頁數 248頁 出版社 上海商務印書館 出版時間 民國25[1936] 出版地點 上海 叢編項 大學叢書 書前冠:序言。—...
《雙曲線·LOVE》是作者王十九(出版該書時署名莫須有)的長篇小說處女作,是一部富有實驗性和時代感的文藝小說。小說中的三名主角粉侯、王泣花和西門小哥在現實...
雙曲線漸近線方程,是一種幾何圖形的算法,這種主要解決實際中建築物在建築的時候的一些數據的處理。雙曲線的主要特點:無限接近,但不可以相交。分為鉛直漸近線、水平...
《雙曲線的殺人案》是海南人民出版社1985年出版的圖書,作者是西村京太郎。...... 《雙曲線的殺人案》是海南人民出版社1985年出版的圖書,作者是西村京太郎。...
