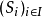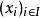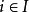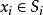基本介紹
- 中文名:選擇公理
- 外文名:Axiom of Choice
- 領域:數學
- 套用:集合論公理
- 簡稱:AC
公理介紹,定義,簡單描述,變體,相關術語,舉例說明,數學化例子,實在例子,沒有答案,爭議,嘗試證明,良序定理,佐恩引理,等價命題,爭論,沒有結論,
公理介紹
非正式地說,選擇公理聲明:給定一些盒子(可以是無限個),每個盒子中都含有至少一個小球,那么可以作出這樣一種選擇,使得可從每個盒子中恰好選出一個小球。在很多情況下這樣的選擇可不藉助選擇公理;尤其是在“盒子個數有限”和“存在具體的選擇規則”(當每個盒子都恰好只有一個小球具有某項特徵)這兩種情況下。再舉一個例子,假設有許多(甚至是無限)雙鞋子,則我們可以選取每雙鞋左邊的鞋子構成一個具體的選擇。然而,假設有無限雙襪子(假設每雙襪子都沒有可區分的特徵),在這種情況下,有效的選擇只能通過選擇公理得到。
儘管曾具有爭議性,選擇公理現在已被大多數數學家毫無保留地使用著,例如帶有選擇公理的策梅洛-弗蘭克爾集合論(ZFC)。數學家們使用選擇公理的原因是,有許多被普遍接受的數學定理,比如是吉洪諾夫定理,都需要選擇公理來證明。現代的集合論學家也研究與選擇公理相矛盾的公理,例如決定公理。
在一些構造性數學的理論中會避免選擇公理的使用,不過也有的將選擇公理包括在內。
定義
首先定義幾個概念:
1)集族:指由非空集合組成的集合。
那么,選擇公理表示:
- 對於所有的集族,均存在選擇函式。
上述可表示為:
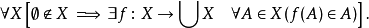
設X是一個集族,則存在著在X上定義的一個選擇函式f。
該定理也可表達為:集族上的任意笛卡爾積總是非空的。
簡單描述
選擇公理有很多等價的形式(equivalent form),以下用一個較簡單的描述:
選擇公理:
變體
1.第二個版本的選擇公理聲稱:
給定由相互不交的非空集合組成的任何集合,存在著至少一個集合,它與每個非空集合恰好有一個公共元素。
2.第三個版本聲稱:
使用這個版本的作者通常談及“在A上的選擇函式”,但要注意這裡選擇函式的概念是稍微不同的。它的定義域是A的冪集(減去空集),因此對任何集合A有意義;至於本文中其他地方用的定義,在“集合的蒐集”上的選擇函式的定義域是這個蒐集,所以只對集合的集合有意義。
透過這個變體的定義,選擇公理也可以簡潔的陳述為:所有集合有一個選擇函式。它等價於對於任何集合A有一個函式使得對於A的任何非空子集B,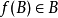 。
。
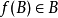
而選擇公理的否定表達為:有一個集合A使得對於所有函式f(在A的非空子集的集合上),有一個B使得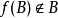 。
。
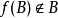
相關術語
以下列出了這篇條目中各種與選擇公理相關的縮寫:
1)AC: 選擇公理。
2)ZF:策梅洛-弗蘭克爾集合論,不包括選擇公理。
3)ZFC:策梅洛-弗蘭克爾集合論,包括選擇公理。
舉例說明
為令讀者有進一步的了解,以下是一些例子:
數學化例子
2a. 如果C為所有長度有限而非零的實數區間的集合,那么,我們可以定義一個新集合,使得它的元素為每一個C中的區間的中間點和所在區間配成的有序對。
實在例子
看來也算是合理,但以上的例可能較數學化、較難理解,現在再用個較實在的例子,
3a. 如果在前面放了放置了幾堆蘋果。那么,我們可以在每堆中選取一個蘋果,再把它們放在新的一堆內。
看了這個例子,可能令你更加明白,不過要留意的是所謂“幾堆”,可能是無限堆,而每堆蘋果也可能是有無限個的,那么,可以換成
3b. 如果在前面放了放置了無限堆蘋果,而每堆蘋果也有無限個。那么,我們可以在每堆中選取一個蘋果,再把它們放在新的一堆內。
這個便是“選擇公理”。看來也很合理,既然每一堆也是有蘋果的,當然可以在每一堆中選擇一個蘋果出來,不論每堆的蘋果數目的多少,和堆數的多少,“應該”也能做到。
但在這堆蘋果中,究竟選擇那一個呢?或許有人會說:“隨便一個便可!”但什麼是“隨便”呢?可否具體點陳述出來呢?這個“隨便”的方法是否必然存在呢?
2b. 如果C為所有長度非零的實數區間,那么,我們可以定義一個新集合,使得它的元素為每一個C中的區間中的點和所在區間配成的有序對。
如果仔細的看2b,“每一個C中的區間中的點”,哪一點呢?最大的那一點?最小的那一點?中間的那一點?通通也不存在,因為“長度非零的實數區間”是包括了長度無限的區間,那便可能沒有了所謂“最大”、“最小”或“中間”等概念。那么,如何具體地陳述出方法呢?這個方法會不會不存在呢?
這個問題可能還是可以回答的,只是要複雜一些,將集合分為3類:有限的取中間點,一面無限的取另一面的邊界+1或-1,而(-∞,+∞)中取0。
沒有答案
然而下面的問題就確實無法給出答案:
可能有人認為,即使是不能陳述出方法,也不能因此就否定或放棄這公理,因為在數學上有很多“存在性定理”(Existence Theorems),都是只指出某事件的存在性,而不具體描述尋求的方法,例如:中值定理(Mean Value Theorem)及洛爾定理(Rolle's Theorem),都是已證明是正確的存在性定理,所以只要能證明這公理是正確,便可以繼續使用。
另外,不能具體陳述出方法,也有可能是括限於人類在語言上的障礙,也即是說,只是不能用人類的語言表達而已,正如最偉大的文學家,也只是用他們認為最適當的語句來表達,可能受到語言限制,不能完全反映他們內心的思想,正所謂“不能言喻”。
爭議
嘗試證明
但“選擇公理”當然不是這般簡單,它的不可思議,它的奇妙用法,以及它所導致的結果,到現在才是開始。
要證明選擇公理,並非一件容易的事,其中一個原因是選擇公理不單是一條簡單的數學命題,而是牽涉較基層的數學──集合論。而集合論正就是數學的基礎理論,所以在證明時,工具也會較少。
不少的數學家也曾嘗試證明選擇公理,他們希望用最基本的工具來作證明,但往往在這些證明中,都用了一些並不基本的理論,例如:“良序定理”(Well-ordering Theorem)及“佐恩引理”(Zorn's Lemma),
良序定理
佐恩引理
若一偏序集是歸納序集,那么,它必然存在最大元素。換句話說,如果在一個偏序集的每一條鏈在原來的偏序集中都存在著上界,這偏序集必存在最大元素。
等價命題
更有趣的結果是原來“選擇公理”、“良序原理”及“佐恩引理”都是等價的命題,也就是說它們是在描述同一樣的事件。多年以來,所發現的“選擇公理”的等價命題實在不少,網主並沒有統計過,某些的書籍可寫出約30個等價命題,網主亦蒐集了部分等價命題(英文版)可供網友參考,而人類只是在這些命題與命題間兜兜轉轉。
爭論
由此可知,要在數學上證明或否證“選擇公理”並非易事,所以數學家便轉移目標,從邏輯系統中看看它的相容性。而事實上,經證明所得,現在我們常用的ZF公理系統與“選擇公理”是相容的,也就是說用ZF公理系統不能得出“選擇公理”的邏輯矛盾。如果我們選擇接納“選擇公理”,則便有一套包含“選擇公理”的公理系統,一般稱“ZFC公理系統”;否則,便不接納它在公理系統之內,在能把它證明之前,也不能接受它是一“定理”。
不過,這個爭論依然未完,因為對於這條公理不只是接納和不接納的問題,如果放棄這條公理,有很多美好且乎合“常理”的結果會同時被放棄;但它實際上又與很多“常理”大不協調。
這其實也是牽涉另一個數學概念──可測集合(Measurable Set)。“巴拿赫─塔斯基悖論”便是存在不可測集合的結果。如果我們接納“選擇公理”,則我們必須接納不可測集合。若我們不接納“選擇公理”,則可設所有集合皆是“勒貝格可測的”(Lebesgue Measurable),而這個假設也可能是較合乎常理。
但是,如果放棄選擇公理,也會有一些很不合常理的情況出現。這些情況取決於選定的不符合選擇公理的模型。如在Cohen模型中,存在一個函式,它在一點x0處是不連續的,但對於任何極限為x0的數列{an},{bn=f(an)}的極限都是f(x0)。換句話說,用任何逼近x0的數列時,函式值都能逼近f(x0),而這恰恰是“連續性”的體現。有些模型更是否定“二元可數選擇公理”(可數個二元集合上選擇公理成立),而這條公理等價於“可數個不交二元集的並集可數”!
沒有結論
總而言之,“選擇公理”是一條十分爭議性的命題,一般的數學家都接受這條公理,因為可以從而得出很多有用的結果,反正使用這公理是沒有邏輯矛盾的。但對於邏輯家或集合論家來說,這是一個必須解決的問題,有些人會建議用較弱的“可數選擇公理”(Countable Choice)來代替,而確實有很多結果是可以利用可數選擇公理來證明的,不過這樣只是暫時迴避問題,而且依然有些結果是必須用到“選擇公理”的。
著名哲學家兼數學家羅素(Bertrand Russell)曾說過:“由無限雙襪子中,每雙選擇一隻出來的話,我們需要‘選擇公理’,但如果換成是鞋的話,那便不必了。”因為鞋是可以分左右的,襪子則兩隻沒什麼分別,不知如何選擇。另外,如果只有有限雙襪子,在邏輯上是可以不用“選擇公理”的。
邦拿(Jerry Bona)也曾說過:“‘選擇公理’明顯是正確的;‘良序原理’明顯是不正確的;‘佐恩引理’又有誰可決定呢?”這雖然是一個笑話,但從此可知道人的直覺並不一定跟從數學的思維。在數學上,這三個命題是等價的,但對於“選擇公理”,很多數學家都直覺它是正確的;對於“良序原理”,很多數學家都認為存在問題;“佐恩引理”則複雜得很多數學家也不能單憑直覺作判斷。
“選擇公理”確是一條謎樣的公理,雖然看似十分淺顯,但卻有奇妙的功能,甚至有超乎常理的結果。有些人對它投以信任一票,有些人則抱懷疑態度。有關這條公理的討論和研究,相信還會繼續,那便看看數學家如何把它解決。最後,網主用羅素的一句話作結束,他在談及“選擇公理”時曾說:
“起先它似乎是明白的;但你愈多思考它,由這公理得出的推論就好像變得愈奇怪;最後你完全不明白它的意思到底是甚么了。”