基本介紹
- 中文名:矩陣行列式
- 外文名:determinant of a matrix
- 所屬學科:數學
- 所屬問題:高等代數(矩陣)
- 簡介:矩陣的全部元素構成的行列式
基本介紹
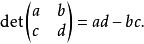
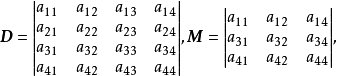

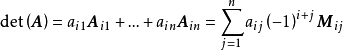
相關定理
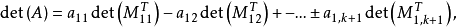
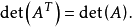

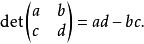
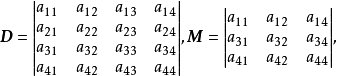

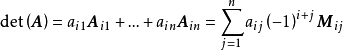
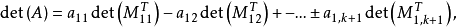
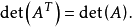
矩陣行列式(determinant of a matrix)是指矩陣的全部元素構成的行列式,設A=(aij)是數域P上的一個n階矩陣,則所有A=(aij)中的元素組成的行列式稱為矩陣A的...
行列式在數學中,是一個函式,其定義域為det的矩陣A,取值為一個標量,寫作det(A)或 | A | 。無論是線上性代數、多項式理論,還是在微積分學中(比如說換元積分...
如右圖利用加減消元法,為了容易記住其求解公式,但要記住這個求解公式是很困難的,因此引入三階行列式的概念。記稱左式的左邊為三階行列式,右邊的式子為三階行列式的...
矩陣的行列式是支持Android 1.6的軟體,該數學應用程式能夠計算矩陣的行列式。...... 矩陣的行列式是支持Android 1.6的軟體,該數學應用程式能夠計算矩陣的行列式。...
n個未知數n個線性方程所組成的線性方程組,它的係數矩陣的行列式叫做係數行列式(determinant of coefficient)。...
在數學中,矩陣(Matrix)是一個按照長方陣列排列的複數或實數集合,最早來自於方程組的係數及常數所構成的方陣。這一概念由19世紀英國數學家凱利首先提出。矩陣是高等...
矩陣單位,即單位矩陣。線上性代數中,n階單位矩陣,是一個n*n的方形矩陣,其主對角線元素為1,其餘元素為0。...
線上性代數中,迪厄多內行列式是矩陣與除環和局部環上矩陣的行列式的推廣。 它是在1943年由迪厄多內提出的。...
線性變換行列式是一種特殊行列式,指線性變換矩陣的行列式。設σ是數域P上的n維線性空間V的線性變換,因為相似矩陣有相等的行列式,所以可以把σ關於V的任意基的矩陣的...
行列式在數學中,是由解線性方程組產生的一種算式。行列式的特性可以被概括為一個多次交替線性形式,這個本質使得行列式在歐幾里德空間中可以成為描述“體積”的函式。...
一個e階的范德蒙行列式由e個數c₁,c₂,…,cₑ決定,它的第1行全部都是1,也可以認為是c₁,c₂,…,cₑ各個數的0次冪,它的第2行就是c₁,c...
將矩陣的行列互換得到的新矩陣稱為轉置矩陣,轉置矩陣的行列式不變。...... 將矩陣的行列互換得到的新矩陣稱為轉置矩陣,轉置矩陣的行列式不變。中文名 轉置矩陣 外...
函式行列式是n元函式對每個自變數求偏導數構成的n維矩陣的行列式,也被稱為雅克比行列式。它是坐標變換理論下的基礎內容之一,不僅在數學分析隱函式理論中發揮著重要的...
矩陣的秩是線性代數中的一個概念。線上性代數中,一個矩陣A的列秩是A的線性獨立的縱列的極大數。通常表示為r(A),rk(A)或rank A。線上性代數中,一個矩陣A...
矩陣變換是線性代數中矩陣的一種運算形式。線上性代數中,矩陣的初等變換是指以下三種變換類型 :(1) 交換矩陣的兩行(對調i,j,兩行記為ri,rj);(2) 以一個非...
設A 是n階方陣,如果存在數m和非零n維列向量 x,使得 Ax=mx 成立,則稱 m 是矩陣A的一個特徵值(characteristic value)或本徵值(eigenvalue)。...
雅可比行列式通常稱為雅可比式(Jacobian),它是以n個n原函式的偏導數為元素的行列式 。事實上,在函式都連續可微(即偏導數都連續)的前提之下,它就是函式組的微分...
在向量微積分中,雅可比矩陣是一階偏導數以一定方式排列成的矩陣,其行列式稱為雅可比行列式。雅可比矩陣的重要性在於它體現了一個可微方程與給出點的最優線性逼近。...
格拉姆矩陣是半正定的,反之每個半正定矩陣是某些向量的格拉姆矩陣。這組向量一般不是惟一的:任何正交基的格拉姆矩陣是恆同矩陣。...
初等矩陣是指由單位矩陣經過一次三種矩陣初等變換得到的矩陣。初等矩陣的模樣可以寫一個3階或者4階的單位矩陣。首先:初等矩陣都可逆,其次,初等矩陣的逆矩陣其實是一...
