基本介紹
- 中文名:矩陣範數
- 外文名:matrix norm
- 別名:相容範數
- 規定:必須滿足相容性
- 性質:正定性,齊次性和三角不等式
- 套用學科:數學
定義
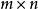
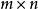

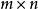
- ||A||>=0;
- ||A||=0 iff A=O (零矩陣); (1和2可統稱為正定性)
- ||aA||=|a| ||A||; (齊次性)
- ||A+B||<= ||A|| + ||B||. (三角不等式)
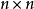
擴展
誘導範數
非誘導範數
酉不變範數
範數的等價
等價
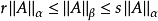

例子
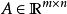
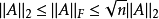
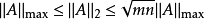


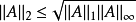

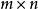
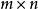

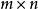
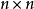
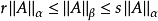

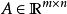
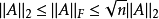
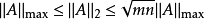


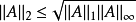
矩陣範數(matrix norm)是數學中矩陣論、線性代數、泛函分析等領域中常見的基本概念,是將一定的矩陣空間建立為賦范向量空間時為矩陣裝備的範數。套用中常將有限維賦...
範數(norm)是數學中的一種基本概念。在泛函分析中,它定義在賦范線性空間中,並滿足一定的條件,即①非負性;②齊次性;③三角不等式。它常常被用來度量某個向量...
二範數指矩陣A的2範數,就是A的轉置共軛矩陣與矩陣A的積的最大特徵根的平方根值,是指空間上兩個向量矩陣的直線距離。類似於求棋盤上兩點間的直線距離。...
在數學中,矩陣(Matrix)是一個按照長方陣列排列的複數或實數集合,最早來自於方程組的係數及常數所構成的方陣。這一概念由19世紀英國數學家凱利首先提出。矩陣是高等...
《矩陣理論及方法》是2012年科學出版社出版的圖書,作者是謝冬秀、雷紀剛、陳桂芝。本書主要介紹了工程實際中有套用價值的矩陣理論與方法。...
《矩陣分析基礎》是2012年出版的圖書,作者是王永茂、劉德友。...... 矩陣的分解、範數及其套用、矩陣分析、矩陣函式、廣義逆矩陣、矩陣的擾動問題簡介,各章末配有...
《矩陣分析與計算》 是國防工業出版社出版的圖書,作者是朱元國。本書主要介紹了矩陣論有關基礎理論,同時,引入矩陣計算的相關內容。...
《矩陣分析》是2005年機械工業出版社出版的圖書,由(美)合恩(Horn.R.A.)創作,楊奇翻譯。該書是一本對數值計算研究人員來說標準的參考書。本書從數學分析的角度...
《矩陣計算(第3版)》是2011年人民郵電出版社出版的圖書,作者是Gene H. Golub Charles F. Van Loan。...
《矩陣數值分析》是2005年1月1日陝西科學技術出版社出版的圖書,作者是邢志棟。...... 本書系統地論述了矩陣數值分析的基本理論和方法。主要內容包括:矩陣和向量的...
BMO範數(BMO norm)記為||f||∗,其中,BMO是有界平均振動之意。...... BMO範數(BMO norm)記為||f||∗,其中...它常常被用來度量某個向量空間(或矩陣)中...
《矩陣論》是2013年清華大學出版社出版圖書。本書比較全面、系統地介紹了矩陣的基本理論、方法及其套用。全書分上、下兩篇,共10章,分別介紹了線性空間與線性運算元,...
厄米特矩陣(Hermitian Matrix,又譯作“埃爾米特矩陣”或“厄米矩陣”),指的是自共軛矩陣。矩陣中每一個第i行第j列的元素都與第j行第i列的元素的共軛相等。...
《工程矩陣理論》是東南大學出版社出版的圖書,作者是張明淳。該書可作為大專院校工科研究生“矩陣論”課程的教材。...
數學定義為矩陣A的條件數等於A的範數與A的逆的範數的乘積,即cond(A)=‖A‖·‖A的逆‖,對應矩陣的3種範數,相應地可以定義3種條件數。...
格式:n=norm(A,p) 功能:norm函式可計算幾種不同類型的矩陣範數,根據p的不同可得到不同的範數...
