基本介紹
- 中文名:正交級數
- 外文名:Fourier series
- 別稱:傅立葉級數
歷史,定義,延伸,希爾伯特空間的解讀,傅立葉級數的收斂性,參閱,
歷史
傅立葉級數得名於法國數學家約瑟夫·傅立葉(1768年–1830年),他提出任何函式都可以展開為三角級數。此前數學家如拉格朗日等已經找到了一些非周期函式的三角級數展開,而認定一個函式有三角級數展開之後,通過積分方法計算其係數的公式,歐拉、達朗貝爾和克萊羅早已發現,傅立葉的工作得到了丹尼爾·伯努利的贊助。傅立葉介入三角級數用來解熱傳導方程,其最初論文在1807年經拉格朗日、拉普拉斯和勒讓德評審後被拒絕出版,他的現在被稱為傅立葉逆轉定理的理論後來發表於1820年的《熱的解析理論》中。將周期函式分解為簡單振盪函式的總和的最早想法,可以追溯至公元前3世紀古代天文學家的均輪和本輪學說。
定義
在這一節中, 表示實變數
表示實變數 的一個函式,且
的一個函式,且 在
在 上可積,
上可積, 和
和 為實數。我們將嘗試用諧波關係的正弦函式的無窮和或級數來表示該區間內的
為實數。我們將嘗試用諧波關係的正弦函式的無窮和或級數來表示該區間內的 。在區間外,級數以
。在區間外,級數以 為周期(頻率為
為周期(頻率為 )。若也具有該性質,則它的近似在整個實數線上有效。我們可以從有限求和(或部分和)開始:
)。若也具有該性質,則它的近似在整個實數線上有效。我們可以從有限求和(或部分和)開始:










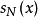


延伸
希爾伯特空間的解讀
所謂的兩個不同向量正交是指它們的內積為0,這也就意味著這兩個向量之間沒有任何相關性,例如,在三維歐氏空間中,互相垂直的向量之間是正交的。事實上,正交是垂直在數學上的一種抽象化和一般化。一組n個互相正交的向量必然是線性無關的,所以必然可以張成一個n維空間,也就是說,空間中的任何一個向量可以用它們來線性表出。
在希爾伯特空間釋義下,函式的集合{en=einx;n∈Z}是[−π,π]平方可積函式L2([−π,π])的正交基。這個空間實際上是一個希爾伯特空間,有著針對任何兩個的元素f和g的如下內積:
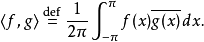



傅立葉級數的收斂性
至今還沒有判斷傅立葉級數的收斂性充分必要條件,但是對於實際問題中出現的函式,有很多種判別條件可用於判斷收斂性。比如x(t)的可微性或級數的一致收斂性。在閉區間上滿足狄利克雷條件的函式表示成的傅立葉級數都收斂。狄利克雷條件如下:
- 在定義區間上,x(t)須絕對可積;
- 在任一有限區間中,x(t)只能取有限個極值點;
- 在任何有限區間上,x(t)只能有有限個第一類間斷點。
滿足以上條件的x(t)傅立葉級數都收斂,且:
1.當t是x(t)的連續點時,級數收斂於x(t);
2.當t是x(t)的間斷點時,級數收斂於

1966年,里納特·卡爾松證明了勒貝格二次可積函式的傅立葉級數一定是幾乎處處收斂的,即級數在除了一個勒貝格零測集外均收斂。
至今還沒有判斷傅立葉級數的收斂性充分必要條件,但是對於實際問題中出現的函式,有很多種判別條件可用於判斷收斂性。比如x(t)的可微性或級數的一致收斂性。在閉區間上滿足狄利克雷條件的函式表示成的傅立葉級數都收斂。狄利克雷條件如下:
- 在定義區間上,x(t)須絕對可積;
- 在任一有限區間中,x(t)只能取有限個極值點;
- 在任何有限區間上,x(t)只能有有限個第一類間斷點。
滿足以上條件的x(t)傅立葉級數都收斂,且:
1.當t是x(t)的連續點時,級數收斂於x(t);
2.當t是x(t)的間斷點時,級數收斂於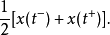
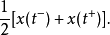
1966年,里納特·卡爾松證明了勒貝格二次可積函式的傅立葉級數一定是幾乎處處收斂的,即級數在除了一個勒貝格零測集外均收斂。
參閱
- 離散時間傅立葉級數
- 維爾斯特拉斯逼近定理
