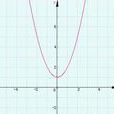
一般地，如果對於函式f(x)的定義域內任意的一個x，都有f(x)=f(-x),那么函式f(x)就叫做偶函式(Even Function)。
基本介紹
- 中文名：偶函式
- 外文名：Even function
- 形式：f(x)=f(-x)
- 特性：
來源,公式,判定方法,代數判斷法,幾何判斷法,運算法則,
來源
最早的奇偶函式的定義
1727年，年輕的瑞士數學家歐拉在提交給聖彼得堡科學院的旨在解決“反彈道問題”的一篇論文（原文為拉丁文）中，首次提出了奇、偶函式的概念。若用-x代替x,函式保持不變，則稱這樣的函式為偶函式(拉丁文functionespares)。歐拉列舉了三類偶函式和三類奇函式，並討論了奇偶函式的性質。法國 數學家達朗貝 爾(J.R.D.Alembert，1717-1783)在狄德羅(D.Diderot,1713-1784)主編的《大百科全書》第7卷（1757年出版）關於函式的詞條中說：“古代幾何學家，更確切地說 是古代分析學家，將某個量x的不同次冪稱為x的函式．”類似地，法國數學家拉格朗日《解析函式論》（1797）開篇中也說，早期分析學家們使用“函式”這個詞，只是表示“同一個量的不同次冪”，後來，其涵義被推廣，表示“以任一方式得自其他量的所有量”，萊布尼茨和約翰· 伯努利最早採用了後一涵義。在1727年的論文中，歐拉在討論奇、偶函式時確實沒有涉及任何超越函式。因此，最早的奇、偶函式概念都是針對冪函式以及相關複合函式而言，歐拉提出的“ 奇函式”、“偶函式”之名顯然源於冪函式的指數或指數分子的奇偶性：指數為偶數的冪函式為偶函式， 指數為奇數的冪函式為奇函式。
《無窮分析引論》中的奇、偶函式概念
1748年,歐拉出版他的數學名著《無窮分析引論》，將函式確立為分析學的最基本的研究對象．在第一章，他給出了函式的定義、對函式進行了分類，並再次討論了兩類特殊的函 數：偶函式和奇函式。歐拉給出的奇、偶函式定義與1727年論文中的定義實質上並無二致，但他討論了更多類型的奇、偶函式，也給出了奇函式的更多的性質。
歐拉的困惑和失誤
歐拉認為，函式
與函式
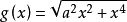是等價的，所以儘管奇函式與偶函式的乘積為奇函式，但有時這樣的乘積也可能會是偶函式。鑒於此，歐拉提出，要使一個偶函式的冪仍為偶函式，就必須對冪指數進行限制，特別的，如果指數為分數， 那么它的分母就不能為偶數。在將偶函式定義為
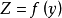和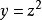
的複合函式時，歐拉特別增加了一個限制條件：
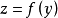中不能含有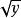
之類的根式。顯然，歐拉未能區別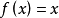函式
和函式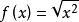
。
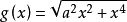
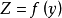
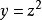
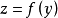
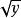
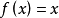
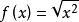
法文和英文中的奇偶函式
1786年 ，法國人裴奇（F.pezzi）將《 無窮分析引論》 第1卷譯成了法文，“奇函式”和“偶函式”分別被譯為“fonction paire”“fonction impaire”,這是兩個數學名詞在法文中的首次出現。
“奇函式”、“偶函式”這兩個名稱在18世紀末的法國並未得到普遍使用；或者說，函式的奇偶性還沒有受到當時法國數學家的普遍關注。1796年，法國數學家拉貝將《無窮分析引論》全書譯成法文，其中拉貝同樣將“奇函式”、“偶函式”分別譯為“fonction paire”“fonction impaire”
1809年，蘇格蘭數學家華里司（W.Wallace,1768-1843）將勒讓德的論文譯成英文， 發表在《數學文庫》(MathematicsRepository)上。華里司很自然地將 “function paire”譯為“even function”。這是“even function”這個詞在英語世界中的首次出現。不過，在英國著名數學家胡頓 （C.Hutton，1737-1823）於1815年出版的《數學與哲學辭典》中，雖然有“函式”和“微積分中的函式”這兩個詞條，但奇、偶函式念卻付之闕如。而德摩根的《代數學基礎》（偉烈亞力和李善蘭譯為《代數學》）雖對函式進行了清晰地分類，但仍隻字未提奇、偶函式。在美 國，數學家羅密士（E.Loomis,1811-1889）的微積分暢銷書《解析幾何與微積分基礎》（李善蘭與偉烈亞力譯為《代微積拾級》）雖然給出了隱函式、顯函式、增 函 數、減函式之名，但同樣不含奇、偶函式之說。這說明，奇、偶函式概念以及華里司所引入的新名詞在19世紀上半葉的英語世界裡尚未得到廣泛傳播和普遍關注．相應地，兩個概念也就不見於中國晚清的西方數學譯著。直到20世紀初，兩個概念才傳入中國。1938年出版的《算學名辭彙編》 和1945年出版的《數學名詞》 中都收錄了兩個名詞。
公式
1、如果知道函式表達式,對於函式f(x)的定義域內任意一個x，都滿足 f(x)=f(-x) 如y=x*x；
2、如果知道圖像,偶函式圖像關於y軸（直線x=0）對稱.
3、定義域D關於原點對稱是這個函式成為偶函式的必要不充分條件.
例如:f(x)=x^2,x∈R，此時的f(x)為偶函式.f(x)=x^2,x∈(-2,2](f(x)等於x的平方,-2<x≤2),此時的f(x)不是偶函
數。
判定方法
代數判斷法
主要是根據奇偶函式的定義，先判斷定義域是否關於原點對稱，若不對稱，即為非奇非偶，若對稱，f(-x)=-f(x)的是奇函式； f(-x)=f(x)的是偶函式。
幾何判斷法
關於原點對稱的函式是奇函式，關於Y軸對稱的函式是偶函式。
如果f(x)為偶函式，則f(x+a)=f[-(x+a)]
但如果f(x+a)是偶函式，則f(x+a)=f(-x+a)
運算法則
(1) 兩個偶函式相加所得的和為偶函式.
(2) 兩個奇函式相加所得的和為奇函式.
(3) 一個偶函式與一個奇函式相加所得的和為非奇函式與非偶函式.
(4) 兩個偶函式相乘所得的積為偶函式.
(5) 兩個奇函式相乘所得的積為偶函式.
(6) 一個偶函式與一個奇函式相乘所得的積為奇函式.
(7)奇函式一定滿足f(0)=0（因為F（0）這個表達式表示0在定義域範圍內，F(0)就必須為0）所以不一定奇函式有f(0)，但有F（0）時F（0）必須等於0，不一定有f(0)=0，推出奇函式，此時函式不一定為奇函式，例f(x)=x^2.
(8)定義在R上的奇函式f（x）必滿足f（0）=0；因為定義域在R上，所以在x=0點存在f(0)，要想關於原點對稱，在原點又只能取一個y值，只能是f(0)=0。這是一條可以直接用的結論：當x可以取0，f（x）又是奇函式時，f（0）=0）。
(9)若且唯若f（x）=0（定義域關於原點對稱）時，f（x）既是奇函式又是偶函式。
(10) 在對稱區間上，被積函式為奇函式的定積分為零。
