基本介紹
- 中文名:點集拓撲
- 外文名:Point Set Topology
- 領域:拓撲學
定義
研究範圍
- 緊緻性和連續性
- 可數性公理
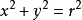
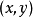
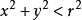
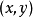
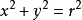
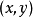
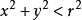
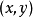
點集拓撲學(Point Set Topology),有時也被稱為一般拓撲學(General Topology),是數學的拓撲學的一個分支。它研究拓撲空間以及定義在其上的數學結構的基本性質。這...
點集拓撲學(Point Set Topology),又名一般拓撲學(General Topology),是用點集的方法研究拓撲不變數的拓撲學分支,主要處理的基本概念是:“連續性”,“緊性”和“...
《點集拓撲講義(第4版)》是 2011年6月1日高等教育出版社出版的圖書。本書可作為數學類專業拓撲學課程的教材或教學參考書。...
點集拓撲法又稱一般拓撲法,是主要用來研究拓撲空間的自身結構及其間的連續映射的方法。在19世紀70年代德國數學家康托爾(G.Cantor)建立集合論後,20世紀初法國數學...
歐氏空間中的點集的研究,例如,一直是拓撲學的重要部分,已發展成一般拓撲學與代數拓撲學交匯的領域,也可看作幾何拓撲學的一部分。50年代以來,即問兩個映射,以R....
《高等學校教材:點集拓撲講義》是2003年高等教育出版社出版的圖書,作者是熊金城 。...... 《高等學校教材:點集拓撲講義》是2003年高等教育出版社出版的圖書,作者是...
淺論點集拓撲、曲面和微積分拓撲內容簡介 編輯 微分拓撲學是當代數學的光輝篇章之一,本書向讀者介紹這門高深的數學。著重在說明大意,不拘泥於嚴格證明,使讀者能...
譯者對原書個別定理證明中不夠清楚的地方,稍作改動。本書可作數學系高年級學生拓撲學課程的教學參考書。[1] 參考資料 1. 點集拓撲學原理 .豆瓣[引用日期2017-...
《點集拓撲與代數拓撲引論》是2013年出版的圖書,作者是包志強。...... 點集拓撲與代數拓撲引論主要內容 編輯 書號: 23060 ISBN: 978-7-301-23060-2 作者: 包志...
一個分支是偏重於用分析的方法來研究的,叫做點集拓撲學,或者叫做分析拓撲學。另一個分支是偏重於用代數方法來研究的,叫做代數拓撲。現在,這兩個分支又有統一的...
本書可作為綜合大學、高等師範院校數學系的拓撲課教材,也可供有關的科技人員和拓撲學愛好者作為課外學習的入門讀物。本書是拓撲學的入門教材。內容包括點集拓撲與...
本書主要討論離散半動力系統,第7章把離散系統的弱幾乎周期點概念推廣到流的情形.前兩個附錄分別介紹必備的集合論和點集拓撲以及遍歷理論知識,而附錄C則是一篇深入...
《淺論點集拓撲曲面和微積分拓撲》是1998年湖南教育出版社出版的圖書,作者是楊忠道。...
圖集 《淺論點集拓撲曲面和微積分拓撲》圖冊 V百科往期回顧 詞條統計 瀏覽次數:次 編輯次數:1次歷史版本 最近更新: 創建者:w_ou猜...
在拓撲學中,同胚(homeomorphism、topological isomorphism、bi continuous function)...點集拓撲系列 參考資料 1. 江澤涵. 拓撲學引論[M]. 上海科學技術出版社, ...
積分流形(integral manifold)是一類子流形。它是由對合分布確定的子流形。流形是一類拓撲空間,它在每一點的附近都與歐氏空間同胚。一般的流形概念,起始於對於可...
道路連通空間(path connected space)是一類拓撲空間,若對於拓撲空間X中的任意兩點都存在以這兩點分別為始點與終點的道路,則稱X為道路連通空間。若拓撲空間的子集...
教學方面,主講過本科生的數學分析、常微分方程、數學分析研究、點集拓撲以及研究生的泛函分析、偏微分方程、非線性泛函、抽象空間積分方程等課程·...
6 序列充分多的拓撲分子格乘積與直積的若干性質,東北數學,1989, Vol. 5, No. 3,337-342(核心期刊)7 可數強F-緊集的刻畫與性質, 模糊系統和數學,2000, ...
局部連通空間 (locally connected space),是一類拓撲空間,它由連通子集組成的的鄰域基及連通分支等組成。設X為拓撲空間X,若存在由連通子集組成的x的鄰域基,則稱...
4 國家自然科學基金 (數學天元基金) 集論拓撲 劉應明3 國家優秀專著出版基金 廣義度量空間與映射 林壽2國家自然科學基金 (數學天元基金) 19476010 點集拓撲 林壽...
