微分拓撲學是研究微分流形在微分同胚映射下不變的性質的數學分支。研究的基本對象是微分流形或帶邊的微分流形以及這樣的流形之間的可微映射。
基本介紹
- 中文名:微分拓撲學
- 外文名:differential topology
- 適用範圍:數理科學
簡介,發展,微分同胚,微分嵌入,協邊,
簡介
微分流形除了是拓撲流形外,還有一個微分結構。因此,對於從一個微分流形到另一個微分流形的映射,不僅可以談論它是否為連續,還可以談論它是否可微分。
微分拓撲的奠基人是H.惠特尼,他研究的主要課題有微分同胚、微分浸入、微分嵌入、協邊理論等。
發展
微分拓撲學早期的研究可以追溯到拉格朗日(J.L.Langrange)、黎曼(B.Riemann).龐加萊(H.Poincare) 的不同時期。但由於數學工具的限制,相當長一段時間微分流形的研究未取得突破性進展。直到惠特尼(H.Whitney)1935 年給出了微分流形的一般定義並證明它總能嵌入到高維歐幾里得空間作為子流形,以及凱恩斯(S.S.Cairns) 證明了微分流形的可剖分性,才使對其的研究重新興起。觸發了莫爾斯理論的產生,奇點理論這一分支的誕生。
伴隨著代數拓撲學中同調及上同調理論、纖維叢理論、示性類理論以及同倫倫的研究進展,1953 年托姆(R.Thom) 建立了協邊理論,開創了微分拓撲學與代數拓撲學並肩躍進的局面,使得許多困難的微分拓撲問題被化成代數拓撲問題而得到解決,同時也刺激了代數拓撲學的進一步發展。
1956 年米爾諾(J.w.Milnor) 發現7 維球面上除了通常的微分結構之外.還有不同尋常的微分結構。隨後,凱瓦雷(M.A.Kervaire) 構造出了不能賦以任何微分結構的流形。這些都顯示拓撲流形、微分流形以及介於其間的分段線性流形這三個範疇有巨大的差別,微分拓撲學也從此被公認為一個獨立的拓撲學分支,並進入20 世紀數學發展的主流。
1960 年斯梅爾(S.Smale) 證明了 5 維以上微分流形的龐加萊猜想。米爾諾(J.W.Milnor)等發展了處理微分流形的基本方法一一剜補術,導致手術理論的產生,使得 5 維以上流形的分類問題亦逐步趨向代數化。
近 30 多年以來,在微分流形的研究中,突出的領域如流形的上述三大範疇之間的關係以及三維、四維流形的分類。 80 年代初的重大成果有:弗里德曼(M.H.Freedman) 證明了四維龐加萊猜想,以及 4 維歐幾里得空間及 4 維流形上有不同尋常的微分結構的發現等。 2003 年佩雷爾曼(G.Perelman)宣布證明了三維龐加萊猜想。
微分同胚
微分流形M和N叫做是微分同胚的,如果存在M和N之間的一一對應ƒ:M→N,使得ƒ和它的逆映射ƒ-1:N→M 都是可微映射。在微分拓撲中,彼此微分同胚的流形被看作是等價的。把等價的微分流形看作屬於同一類。對微分流形進行分類是微分拓撲最基本的問題。
如果ƒ和ƒ-1僅僅是連續的,不一定可微,則 M 和 N 叫做是同胚的(亦即拓撲上等價的)。同胚的微分流形未必微分同胚。例如,用 S7表示七維球面,即八維歐氏空間 R8中所有單位向量構成的流形,則 S7可被賦以不同的微分結構,使所得的微分流形是不微分同胚的。已經算出,與S7同胚的微分流形,按微
分同胚來分類,一共有 28 類,當 n≥5 時, 與 Sn 同胚的微分流形的等價類的數目,已被證明是有限的,且對 5≤n≤18 ,類數均已被算出(見表)。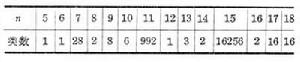 圖1
圖1
 圖1
圖1以Rm表示m維歐氏空間。當m≠4 時,不論以何種方式給Rm 賦以微分結構,所得的微分流形總是微分同胚的。有一個很有意思的事實是,對 R4可賦以不同的微分結構,使所得的微分流形是不微分同胚的。當n=1、2、3 時,任意n維拓撲流形上必可賦以微分結構,且由同一拓撲流形賦以不同的微分結構所得的微分流形必微分同胚。因此,對一、二、三維流形,按微分同胚來分類和按同胚來分類是一樣的。
一維流形的分類很簡單。它們必同胚於開區間 (0,1) ,閉區間 [0,1] ,半開半閉區間 [0,1) 和圓周S1中的一個,且這四個流形必不同胚。二維緊緻無邊流形的分類早已被解決,而三維緊緻無邊流形的分類問題是很困難的,尚未解決。
微分嵌入
設ƒ:M→N是微分映射,如果ƒ(M) 是N的微分子流形,並且ƒ:M→ƒ(M) 是微分同胚,則稱ƒ為微分嵌入。微分嵌入一定是微分浸入。兩個微分嵌入叫做是正則同痕的,如果存在連線它們的正則同倫Ht ,使對每一固定的t∈[0,1],Ht 是微分嵌入。
關於微分嵌入的一個經典結果是:任意n維微分流形可微分嵌入於 2n維歐氏空間中。n≠1,4 時,已證明任意n維可定向的緊緻無邊微分流形可微分嵌入於R 中,n=4 時,可微分嵌入的充分必要條件已發現。
關於S1在 R3 中的微分嵌入按正則同痕分類的問題是很複雜的,已成為一個獨立的研究分支,稱為紐結理論,它密切地關聯於三維流形的同胚分類問題。與S1 在 R3 中的微分嵌入有無窮多個正則同痕類相反,吳文俊證明了:若 n>1 ,則任意 n 維微分流形在 R 中的任意兩個微分嵌入都是正則同痕的。
當n>3(k+1)/2 時,k維微分流形到n維微分流形的微分嵌入的存在和正則同痕分類的問題已被化成同倫論問題,且已證明當k和n滿足上述關係時,S在Rn 中的任意兩個微分嵌入都是正則同痕的,但 S 在R 中的微分嵌入的正則同痕類卻與整數全體一一對應。
協邊
兩個n維的緊緻無邊微分流形M和N叫做是協邊的,如果存在一個n+1 維的緊緻微分流形W,W的邊界恰由M和N 組成。把兩個協邊的微分流形看成屬於同一協邊類,則按協邊關係來分類緊緻無邊微分流形比按微分同胚來分類它們要粗略,因為任意兩個微分同胚的緊緻無邊微分流形必是協邊的。與按微分同胚的精細分類問題至今未能解決形成鮮明對照的是,按協邊關係的粗略分類問題雖非容易,但卻已徹底解決。二維(或三維)的可定向緊緻無邊微分流形都是協邊的,雖然未必微分同胚。實投影平面與二維球面是不協邊的。
上述協邊理論有很多推廣,如可定向流形的協邊論,映射的協邊論,穩定切叢有復結構的流形的協邊論,穩定切叢有標架的流形的協邊論等等。其中標架協邊論與球的同倫群的研究有著互逆的關係,仍是拓撲學中重要的難題。
微分拓撲雖是不同於代數拓撲的一個獨立的數學分支,但它與代數拓撲的關係極為密切。解決微分拓撲問題的許多基本工具,例如同調群、同倫群、拓撲K-理論以及多種示性類等代數不變數都是從代數拓撲中借用過來的。
基於莫爾斯函式的臨界點理論的流形剜補術則是首先對微分流形發展起來的,然後被推廣至拓撲流形的情形。拓撲流形的剜補術在解決四維龐加萊猜想時發揮了作用。可見兩者互相滲透、互相促進。

