基本介紹
- 中文名:矩陣乘法
- 外文名:Matrix multiplication
- 基本性質:結合性 等
- 套用學科:數學,工程學,信息學
- 套用領域:代數,離散
定義



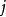
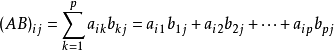
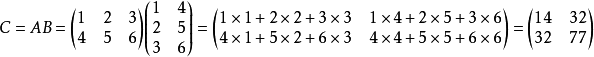
注意事項
基本性質
- 乘法結合律: (AB)C=A(BC).
- 乘法左分配律:(A+B)C=AC+BC
- 乘法右分配律:C(A+B)=CA+CB
- 對數乘的結合性k(AB)=(kA)B=A(kB).
- 轉置 (AB)T=BTAT.
- 矩陣乘法一般不滿足交換律。
其他的乘積形式
哈達馬積(Hadamard product)
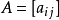
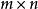
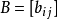


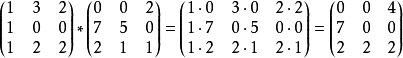
克羅內克積(Kronecker Product)

實現
struct Matrix:vector<vector<int> >//使用標準容器vector做基類,需#include語句{ Matrix(int x=0,int y=0,int z=0)//初始化,默認為0行0列空矩陣 { assign(x,vector<int>(y,z)); } int h_size()const//常量說明不可省,否則編譯無法通過 { return size(); } int l_size()const { return empty()?0:front().size();//列數要考慮空矩陣的情況 } Matrix pow(int k);//矩陣的k次冪,用快速冪實現,k為0時返回此矩陣的單位矩陣};Matrix operator*(const Matrix &m,const Matrix &n)//常量引用避免拷貝{ if(m.l_size()!=n.h_size())return Matrix();//非法運算返回空矩陣 Matrix ans(m.h_size(),n.l_size()); for(int i=0; i!=ans.h_size(); ++i) for(int j=0; j!=ans.l_size(); ++j) for(int k=0; k!=m.l_size(); ++k) ans[i][j]+=m[i][k]*n[k][j]; return ans;}Matrix Matrix::pow(int k){ if(k==0) { Matrix ans(h_size(),h_size()); for(int i=0; i!=ans.h_size(); ++i) ans[i][i]=1; return ans; } if(k==2)return (*this)*(*this); if(k%2)return pow(k-1)*(*this); return pow(k/2).pow(2);}實際套用
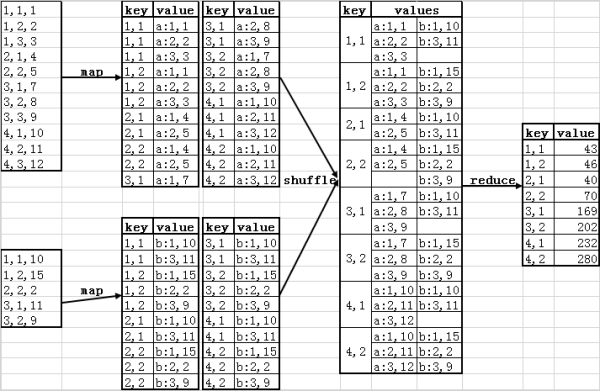
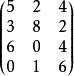
數據統計
| 工廠\產品 | P1 | P2 | P3 |
|---|---|---|---|
甲 | 5 | 2 | 4 |
乙 | 3 | 8 | 2 |
丙 | 6 | 0 | 4 |
丁 | 0 | 1 | 6 |

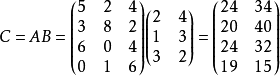
VOJ1067
#include <cmath>#include <cstdio>#include <cstring>#include <iostream>#include <algorithm>#define N 10using namespace std;const int mod = 7777777;typedef long long LL;struct matrix{ LL a[10][10];}origin;int n,m;matrix multiply(matrix x,matrix y){ matrix temp; memset(temp.a,0,sizeof(temp.a)); for (int i=0;i<n;i++) { for (int j=0;j<n;j++) { for (int k=0;k<n;k++) { temp.a[i][j]+=x.a[i][k]*y.a[k][j]; temp.a[i][j]=(temp.a[i][j])%mod; } } } return temp;}matrix matmod(matrix A,int k){ matrix res; memset(res.a,0,sizeof res.a); for (int i=0;i<n;i++) res.a[i][i]=1; while(k) { if (k&1) res=multiply(res,A); k>>=1; A=multiply(A,A); } return res;}void print(matrix x){ for (int i=0;i<n;i++) { for (int j=0;j<n;j++) cout<<" "<<x.a[i][j];puts(""); } printf("---------------\n");}int main(){ int k; while (cin>>n>>k) { memset(origin.a,0,sizeof origin.a); origin.a[0][0]=1; for (int i=1;i<=n;i++) { origin.a[i][0]=1; for (int j=0;j<i;j++) origin.a[i][0]+=origin.a[j][0]; } // print(origin); matrix res; memset(res.a,0,sizeof res.a); for (int i=0;i<n-1;i++) res.a[i][i+1]=1; for (int i=0;i<n;i++) res.a[n-1][i]=1; //print(res); res=matmod(res,k-1); LL fans=0; for (int i=0;i<n;i++) { fans+=res.a[0][i]*origin.a[i][0]; fans%=mod; } cout<<fans<<endl; } return 0;}經典題目9
經典題目10
#include <cstdio>#define SIZE (1<<m)#define MAX_SIZE 32using namespace std;class CMatrix{ public: long element[MAX_SIZE][MAX_SIZE]; void setSize(int); void setModulo(int); CMatrix operator* (CMatrix); CMatrix power(int); private: int size; long modulo;};void CMatrix::setSize(int a){ for (int i=0; i<a; i++) for (int j=0; j<a; j++) element[i][j]=0; size = a;}void CMatrix::setModulo(int a){ modulo = a;}CMatrix CMatrix::operator* (CMatrix param){ CMatrix product; product.setSize(size); product.setModulo(modulo); for (int i=0; i<size; i++) for (int j=0; j<size; j++) for (int k=0; k<size; k++) { product.element[i][j]+=element[i][k]*param.element[k][j]; product.element[i][j]%=modulo; } return product;}CMatrix CMatrix::power(int exp){ CMatrix tmp=(*this)*(*this); if (exp==1) return *this; else if (exp&1) return tmp.power(exp/2)*(*this); else return tmp.power(exp/2);}int main(){ const int validSet[]={0,3,6,12,15,24,27,30}; long n, m, p; CMatrix unit; scanf("%d%d%d", &n, &m, &p); unit.setSize(SIZE); for (int i=0; i<SIZE; i++) for (int j=0; j<SIZE; j++) if (((~i)&j) == ((~i)&(SIZE-1))) { bool isValid=false; for (int k=0;k<8;k++) isValid=isValid||(i&j)==validSet[k]; unit.element[i][j]=isValid; } unit.setModulo(p); printf("%d",unit.power(n).element[SIZE-1][SIZE-1] ); return 0;}矩陣乘法例題
#include <cstdio>#include <cstring>#include <algorithm>using namespace std;static const int maxm=1e2+10;#define REP(i,s,t) for(int i=s;i<=t;i++) typedef long long LL;struct matrix{ LL mtx[maxm][maxm];}mx[16];LL n,k,m;LL A[maxm][maxm];matrix mul(matrix A,matrix B){ matrix ret; memset(ret.mtx,0,sizeof ret.mtx); REP(i,1,n)REP(j,1,n)REP(k,1,n) ret.mtx[i][j]=(ret.mtx[i][j]+A.mtx[i][k]*B.mtx[k][j]); return ret;}matrix pow(matrix A,LL n){ if(!n)return A; matrix ret=A;n--; while(n){ if(n&1)ret=mul(ret,A); A=mul(A,A); n>>=1; } return ret;}void display(matrix base){ for(int i=1;i<=n;i++)printf("%lld ",base.mtx[1][i]); puts("");}int main(){ matrix st,get,f; scanf("%lld%lld%lld",&n,&m,&k); for(int i=1;i<=m;i++){ for(int j=1;j<=n;j++){ scanf("%lld",&A[i][j]); mx[i].mtx[A[i][j]][j]=1; } } for(int i=1;i<=n;i++)st.mtx[1][i]=i; get=mx[1]; for(int i=2;i<=m;i++)get=mul(get,mx[i]); get=pow(get,k/m);k%=m; for(int i=1;i<=k;i++)get=mul(get,mx[i]); st=mul(st,get); display(st); return 0;}//by Exbilar