基本介紹
- 中文名:拉格朗日運算元
- 外文名:Lagrange multiplier
- 別稱:拉格朗日乘數、拉格朗日乘子
- 領域:數學
方法介紹,證明,運用方法,經濟學,參考,
方法介紹
在數學中的最最佳化問題中,拉格朗日乘數法(以數學家約瑟夫·拉格朗日命名)是一種尋找多元函式在其變數受到一個或多個條件的約束時的極值的方法。這種方法可以將一個有n個變數與k個約束條件的最最佳化問題轉換為一個解有n+k個變數的方程組的解的問題。這種方法中引入了一個或一組新的未知數,即拉格朗日乘數,又稱拉格朗日乘子,或拉氏乘子,它們是在轉換後的方程,即約束方程中作為梯度(gradient)的線性組合中各個向量的係數。
比如,要求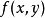 在
在 時的最大值時,我們可以引入新變數拉格朗日乘數
時的最大值時,我們可以引入新變數拉格朗日乘數 ,這時我們只需要下列拉格朗日函式的極值:
,這時我們只需要下列拉格朗日函式的極值:
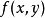




微積分中最常見的問題之一是求一個函式的極大極小值(極值)。但是很多時候找到極值函式的顯式表達是很困難的,特別是當函式有先決條件或約束時。拉格朗日乘數則提供了一個非常便利方法來解決這類問題,而避開顯式地引入約束和求解外部變數。
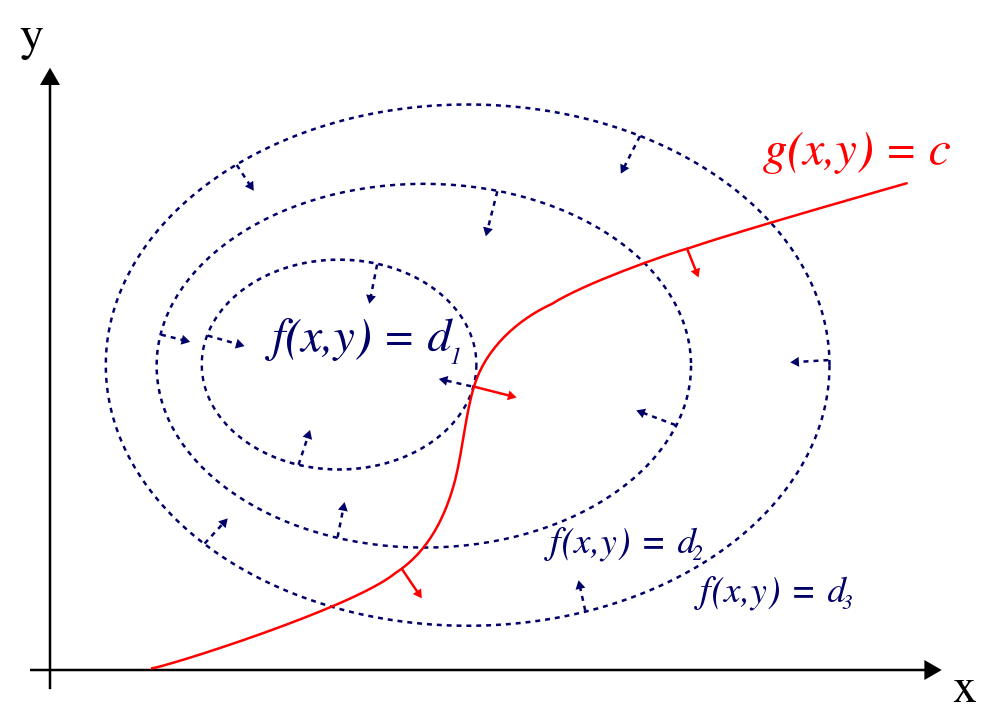
先看一個二維的例子:假設有函式: ,要求其極值(最大值/最小值),且滿足條件
,要求其極值(最大值/最小值),且滿足條件



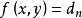












氣象圖中就很常出現這樣的例子,當溫度和氣壓兩列等高線同時出現的時候,切點就意味著約束極值的存在。

一旦求出 的值,將其套入下式,易求在無約束條件下的極值和對應的極值點。
的值,將其套入下式,易求在無約束條件下的極值和對應的極值點。






證明
設函式 在
在 點處有極值
點處有極值 ,且在
,且在 點的鄰域內連續。則在
點的鄰域內連續。則在 點處有
點處有












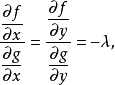





類似地,這種求極值的方法也可以推廣到多維函式 。
。

運用方法
如f定義為在R上的方程,約束為gk(x)=ck(或將約束左移得到gk(x)−ck=0)。定義拉格朗日Λ為




拉格朗日乘數法在卡羅需-庫恩-塔克條件被推廣。
經濟學
拉格朗日乘數就是效用函式在最優解處對收入的偏導數,也就是在最優解處增加一個單位收入帶來的效用增加,或者說在最優解處有效用衡量收入的價值,稱之為收入的邊際效用。
在企業生產問題中,拉格朗日乘數用來衡量要素投入變動所帶來的收入變動, λ表示效用函式或生產函式,m表示收入或要素投入。
λ表示效用函式或生產函式,m表示收入或要素投入。

在具體數學推導中還可以運用包絡定理的內容。
參考
- 卡羅需-庫恩-塔克條件:拉格朗日乘數的推廣。
- 拉格朗日方程式