基本介紹
- 中文名:算符
- 外文名:operator symbol
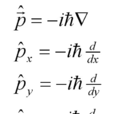
使問題從一種狀態變化為另一種狀態的手段稱為操作符或算符。算符在單獨存在時是沒有什麼意義。操作符可為走步、過程、規則、數學運算元、運算符號或邏輯符號等。....
厄密算符的平均值定理I:體系任何狀態ψ下,其厄密算符的本徵值必為實數。...... 厄密算符的平均值 定理I:體系任何狀態ψ下,其厄密算符的本徵值必為實數。...
算術運算符即算術運算符號。是完成基本的算術運算 (arithmetic operators) 符號,就是用來處理四則運算的符號。...
運算符用於執行程式代碼運算,會針對一個以上運算元項目來進行運算。例如:2+3,其運算元是2和3,而運算符則是“+”。在vb2005中運算符大致可以分為5種類型:算...
算符使問題從一種狀態變化為另一種狀態的手段。算符在單獨存在時是沒有什麼意義,在計算機科學中,算符是指運算符號或邏輯符號等。當前算符是指計算機當前要處理...
對易算符指一組兩兩之間滿足對易關係的算符。而對易運算是一種具有雙線性的運算,本質上類似於李代數。...
微分算符法編輯 鎖定 本詞條特指在陳文燈數學複習指南中提及的解決微分方程的辦法 該方法對於高速解決數學考試中的常微分方程問題效果顯著 其理論來源為拉普拉斯變換...
在量子力學裡,位置算符(position operator)是一種量子算符。對應於位置算符的可觀察量是粒子的位置。位置算符的本徵值是位置矢量。...
當一個粒子在保守力場中運動時,它的勢能與時間無關,此時,體系的能量算符定義為動能算符和勢能算符之和。在保守力場中,體系的能量算符也就是該體系的哈密頓算...
在狹義相對論,電磁學和波理論中,d'Alembert運算符(由一個方框代表,也稱為d'Alembertian或波動運算元或者quabla運算元,是Minkowski空間的拉普拉斯運算元,運算符以法國數學...
物理學中,湮沒算符是將處於特定狀態中的多個粒子,其粒子數下降1的算符;產生算符則是將處於特定狀態中的多個粒子,其粒子數增加1的算符,產生算符也是湮沒算符...
4 注意事項 位運算符簡介 編輯 位運算符用來對二進制位進行操作,Java中提供了如下表所示的位運算符:位運算符中,除~ 以外,其餘均為二元運算符。操作...
時序算符,也常稱為編時算符,在量子場論的格林函式理論中,也被稱為Dyson時序算符。通常記為T,它作用於兩個及其以上的含時算符(或物理量)上,使時間越大的算...
等距算符是一種特殊的算符。...... 圖集 等距算符圖冊 V百科往期回顧 詞條統計 瀏覽次數:次 編輯次數:4次歷史版本 最近更新: 創建者:曾到蝶舞溪...
量子力學中的力學量和算符基本信息 編輯 在量子力學中,當微觀粒子處於某一狀態時,它的力學量(如坐標、動量、角動量、能量等)一般不具有確定的數值,而是具有一...
量子力學中,哈密頓算符(Hamiltonian) H為一個可觀測量(observable),對應於系統的的總能量。一如其他所有算符,哈密頓算符的譜為測量系統總能時所有可能結果的集合...
在數學裡,作用於一個有限維的內積空間,一個自伴運算元(self-adjoint operator)等於自己的伴隨運算元;等價地說,表達自伴運算元的矩陣是埃爾米特矩陣。即厄米算符表達了一...
物理學中,湮沒算符是將處於特定狀態中的多個粒子,其粒子數下降1的算符;產生算符則是將處於特定狀態中的多個粒子,其粒子數增加1的算符,產生算符也是湮沒算符...
場論 二次量子化中產生某個粒子的算符,或由此引申出的具有類似意義的算符。...... 場論 二次量子化中產生某個粒子的算符,或由此引申出的具有類似意義的算符...
在一個表達式中可能包含多個有不同運算符連線起來的、具有不同數據類型的數據對象;由於表達式有多種運算,不同的結合順序可能得出不同結果甚至出現錯誤運算錯誤,因為...
動量算符是在量子力學中表示微觀粒子的動量的算符。動量算符是表示力學量的厄米算符。...
算符 定義 一個函式空間到函式空間上的映射 套用領域 數理科學 目錄 1 運算元解釋 2 常見運算元 3 特徵值 4 可交換 5 認知心理學 運算元...
劈形運算元在數學中用於指代梯度算符,並形成散度、旋度和拉普拉斯運算元。它也用於指代微分幾何中的聯絡(可以視為更廣意義上的梯度運算元)。它由哈密爾頓引入。 [2] ...
異或,英文為exclusive OR,或縮寫成xor異或(xor)是一個數學運算符。它套用於邏輯運算。異或的數學符號為“⊕”,計算機符號為“xor”。其運算法則為:a⊕b = (...
