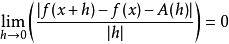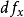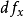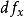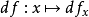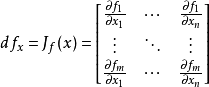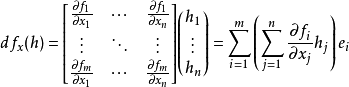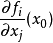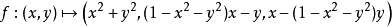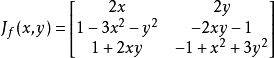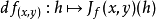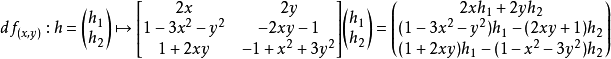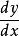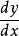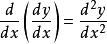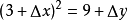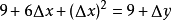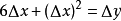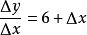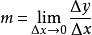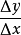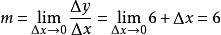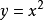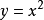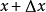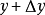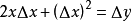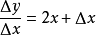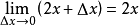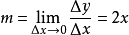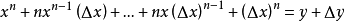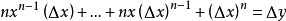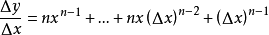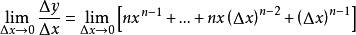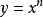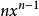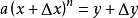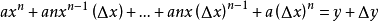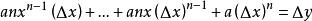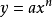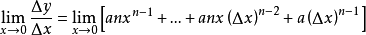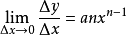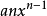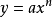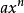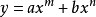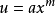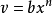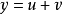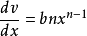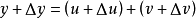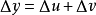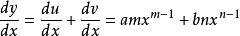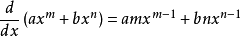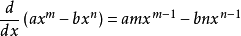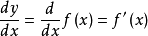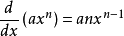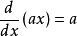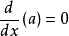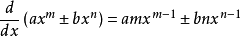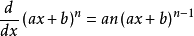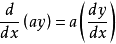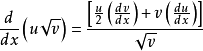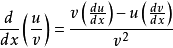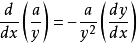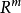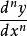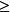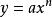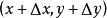微分

微分

微分在數學中的定義：由函式B=f(A)，得到A、B兩個數集，在A中當dx靠近自己時，函式在dx處的極限叫作函式在dx處的微分，微分的中心思想是無窮分割。微分是函式改變數的線性主要部分。微積分的基本概念之一。

基本介紹

  • 中文名：微分
  • 外文名：Differentiation
  • 概述：一種線性描述
  • 一元型：定義 推導
  • 切線微分：當自變數為固定值
  • 運算法則：基本法則 連鎖律 乘法律
  • 歷史：發展歷史
  • 套用科學：數學
發展歷史,一元型,定義,推導,幾何意義,多元型,高階型,定義,性質,例子,切線微分,運算法則,基本法則,連鎖律,乘法律,除法律,導數,導數一,導數二,特殊導數,微分套用,

發展歷史

萌芽時期
早在希臘時期，人類已經開始討論「無窮」、「極限」以及「無窮分割」等概念。這些都是微積分的中心思想；雖然這些討論從現代的觀點看有很多漏洞，有時現代人甚至覺得這些討論的論證和結論都很荒謬，但無可否認，這些討論是人類發展微積分的第一步。
例如公元前五世紀，希臘的德謨克利特（Democritus）提出原子論：他認為宇宙萬物是由極細的原子構成。在中國，《莊子．天下篇》中所言的「一尺之捶，日取其半，萬世不竭」，亦指零是無窮小量。這些都是最早期人類對無窮、極限等概念的原始的描述。
其他關於無窮、極限的論述，還包括芝諾（Zeno）幾個著名的悖論：其中一個悖論說一個人永遠都追不上一隻烏龜，因為當那人追到烏龜的出發點時，烏龜已經向前爬行了一小段路，當他再追完這一小段，烏龜又已經再向前爬行了一小段路。芝諾說這樣一追一趕的永遠重覆下去，任何人都總追不上一隻最慢的烏龜－－當然，從現代的觀點看，芝諾說的實在荒謬不過；他混淆了「無限」和「無限可分」的概念。人追烏龜經過的那段路縱然無限可分，其長度卻是有限的；所以人仍然可以以有限的時間，走完這一段路。然而這些荒謬的論述，開啟了人類對無窮、極限等概念的探討，對後世發展微積分有深遠的歷史意味。
另外值得一提的是，希臘時代的阿基米德（Archimedes）已經懂得用無窮分割的方法正確地計算一些面積，這跟現代積分的觀念已經很相似。由此可見，在歷史上，積分觀念的形成比微分還要早－－這跟課程上往往先討論微分再討論積分剛剛相反。
十七世紀的大發展牛頓和萊布尼茨的貢獻
中世紀時期，歐洲科學發展停滯不前，人類對無窮、極限和積分等觀念的想法都沒有什麼突破。中世紀以後，歐洲數學和科學急速發展，微積分的觀念也於此時趨於成熟。在積分方面，一六一五年，克卜勒（Kepler）把酒桶看作一個由無數圓薄片積累而成的物件，從而求出其體積。而伽利略（Galileo）的學生卡瓦列里（Cavalieri）即認為一條線由無窮多個點構成；一個面由無窮多條線構成；一個立體由無窮多個面構成。這些想法都是積分法的前驅。
在微分方面，十七世紀人類也有很大的突破。費馬（Fermat）在一封給羅貝瓦（Roberval）的信中，提及計算函式的極大值和極小值的步驟，而這實際上已相當於現代微分學中所用，設函式導數為零，然後求出函式極點的方法。另外，巴羅（Barrow）亦已經懂得透過「微分三角形」（相當於以dx、dy、ds為邊的三角形）求出切線的方程，這和現今微分學中用導數求切線的方法是一樣的。由此可見，人類在十七世紀已經掌握了微分的要領。
然而，直至十七世紀中葉，人類仍然認為微分和積分是兩個獨立的觀念。就在這個時候，牛頓和萊布尼茨將微分及積分兩個貌似不相關的問題，透過「微積分基本定理」或「牛頓－萊布尼茨公式」聯繫起來，說明求積分基本上是求微分之逆，求微分也是求積分之逆。這是微積分理論中的基石，是微積分發展一個重要的里程碑。

一元型

定義

設函式y = f(x)在x的鄰域內有定義，x及x + Δx在此區間內。如果函式的增量Δy = f(x + Δx) - f(x)可表示為 Δy = AΔx + o(Δx)（其中A是不隨Δx改變的常量，但A可以隨x改變），而o(Δx)是比Δx高階的無窮小（註：o讀作奧密克戎，希臘字母）那么稱函式f(x)在點x是可微的，且AΔx稱作函式在點x相應於因變數增量Δy的微分，記作dy，即dy = AΔx。函式的微分是函式增量的主要部分，且是Δx的線性函式，故說函式的微分是函式增量的線性主部（△x→0）。
通常把自變數x的增量 Δx稱為自變數的微分，記作dx，即dx = Δx。於是函式y = f(x)的微分又可記作dy = f'(x)dx。函式因變數的微分與自變數的微分之商等於該函式的導數。因此，導數也叫做微商。
當自變數X改變為X+△X時，相應地函式值由f(X)改變為f(X+△X)，如果存在一個與△X無關的常數A，使f(X+△X)-f(X)和A·△X之差是△X→0關於△X的高階無窮小量，則稱A·△X是f(X)在X的微分，記為dy，並稱f(X)在X可微。一元微積分中，可微可導等價。記A·△X=dy，則dy=f′(X)dX。例如：d(sinX)=cosXdX。
微分概念是在解決直與曲的矛盾中產生的，在微小局部可以用直線去近似替代曲線，它的直接套用就是函式的線性化。微分具有雙重意義：它表示一個微小的量，因此就可以把線性函式的數值計算結果作為本來函式的數值近似值，這就是運用微分方法進行近似計算的基本思想。

推導

設函式y = f(x)在某區間內有定義，x0及x0+△x在這區間內，若函式的增量Δy = f(x0 + Δx) − f(x0)可表示為Δy = AΔx + o(Δx)，其中A是不依賴於△x的常數， o(Δx)是△x的高階無窮小，則稱函式y = f(x)在點x0是可微的。 AΔx叫做函式在點x0相應於自變數增量△x的微分，記作dy，即：dy=AΔx。微分dy是自變數改變數△x的線性函式，dy與△y的差是關於△x的高階無窮小量，我們把dy稱作△y的線性主部。得出： 當△x→0時，△y≈dy。 導數的記號為：(dy)/(dx)=f′(X)，我們可以發現，它不僅表示導數的記號，而且還可以表示兩個微分的比值（把△x看成dx，即：定義自變數的增量等於自變數的微分），還可表示為dy=f′(X)dX。

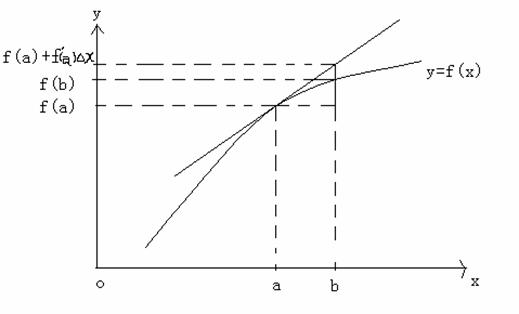
幾何意義

設Δx是曲線y = f(x)上的點M的在橫坐標上的增量，Δy是曲線在點M對應Δx在縱坐標上的增量，dy是曲 線在點M的切線對應Δx在縱坐標上的增量。當|Δx|很小時，|Δy－dy|比|Δx|要小得多(高階無窮小)，因此在點M附近，我們可以用切線段來近似代替曲線段。

多元型

當自變數為多個時，可得出多元微分的定義。一元微分又叫常微分。

高階型

當自變數是多元變數時，導數的概念已經不適用了（儘管可以定義對某個分量的偏導數），但仍然有微分的概念。

定義

設f是從歐幾里得空間（或者任意一個內積空間）中的一個開集射到
的一個函式。對於
中的一點x及其在
中的鄰域
中的點x+h。如果存線上性映射A使得對任意這樣的x+h,
那么稱函式f在點x處可微。線性映射A叫做f在點x處的微分，記作
。
如果f在點x處可微，那么它在該點處一定連續，而且在該點的微分只有一個。為了和偏導數區別，多元函式的微分也叫做全微分或全導數。
當函式在某個區域的每一點x都有微分
時，可以考慮將x映射到
的函式：
這個函式一般稱為微分函式。

性質

如果f是線性映射，那么它在任意一點的微分都等於自身。
在Rn（或定義了一組標準基的內積空間）里，函式的全微分和偏導數間的關係可以通過雅可比矩陣刻畫：
設f是從Rn射到Rm的函式，f=(f1,f2,...fm)，那么：
具體來說，對於一個改變數：
，微分值：
可微的必要條件：如果函式f在一點x_0處可微，那么雅克比矩陣的每一個元素
都存在，但反之不真。
可微的充分條件：如果函式f在一點x_0的雅克比矩陣的每一個元素\frac{\partial f_i}{\partial x_j}(x_0)都在x_0連續，那么函式在這點處可微，但反之不真。

例子

函式
是一個從R2射到R3的函式。它在某一點(x, y)的雅可比矩陣為：
微分為：
，也就是：
我們對函式y進行微分，得出導數
，由於微分只進行了一次，所以
又被稱為一階導數。
這時，我們微分
，得出
，那么
被稱為二階導數。
同理，我們可以得到三次導數及更高次的導數，
（n
2）被稱為n階導數。

切線微分

當自變數為固定值
需要求出曲線上一點的斜率時，前人往往採用作圖法，將該點的切線畫出，以切線的斜率作為該點的斜率。然而，畫出來的切線是有誤差的，也就是說，以作圖法得到的斜率並不是完全準確的斜率。微分最早就是為了從數學上解決這一問題而產生的。
以y=x2 為例，我們需要求出該曲線在(3,9)上的斜率，當△x與△y的值越接近於0，過這兩點直線的斜率就越接近所求的斜率m，當△x與△y的值變得無限接近於0時，直線的斜率就是點的斜率。
當x = 3 +Δx 時，y = 9+ Δy，也就是說，
（展開）
（兩邊減去9）
（兩邊除以△x）
∵
（m為曲線在(3,9)上的斜率，
為直線斜率）
∴
我們得出，
在點(3,9)處的斜率為6。
當自變數為任意值
在很多情況下，我們需要求出曲線上許多點的斜率，如果每一個點都按上面的方法求斜率，將會消耗大量時間，計算也容易出現誤差，這裡我們仍以
為例，計算圖象上任意一點的斜率m。
假設該點為(x,y)，做對照的另一點為(
,
)，我們按上面的方法再計算一遍：
（展開）
（
，兩邊減去y）
（兩邊除以△x）
∵
∴
我們得出，y=x2 在點(x,y)處的斜率為2x。
從二次函式到冪函式
通過以上的方法，我們可以得出x的二次函式在任意一點上的斜率，但是這遠遠不夠。我們需要把這種方法擴充到所有的冪函式。假設有函式
，假設函式上有一點(x,y)和另一點(x+Δx,y+Δy) ，我們可以這樣計算斜率：
（二項展開式）
（
）
（兩邊除以△x）
（加上極限）
（其他項均帶有△x，在△x→0的情況下都可以視為等於0）
我們得出，
在點(x,y)處的斜率為
。
從冪函式到單項式
我們可以把冪函式的斜率擴展到單項式函式
的斜率，依然假設有兩點(x,y)和
：
（二項展開式）
（
,兩邊減去y）
（兩邊除以△x）
（加上極限）
（其他項均帶有△x，在△x→0的情況下都可以視為等於0）
我們得出，
在點(x,y)處的斜率為
。
這就是微分的基本公式，“基本法則”目錄有詳細的說明。
被記作dy/dx=m 。
單項式
當函式為單項式
（a和n為常數）的形式時，有基本公式：
注意：基本公式極為重要，在學習更為複雜的運算法則前請務必牢記。
多項式
當函式為幾個
形式的單項式的和或差時，這個函式的導數只需在原函式的導數上進行加減即可。
以函式
為例，將其拆分為兩個函式
和
，且
。
可以得出
，
。
y=u+v
同理可以得出
最後得出公式：
有了這兩個公式，我們可以對大部分常見的初等函式求導。
注意：f'(x)是函式f(x)的導數。

運算法則

基本法則

連鎖律

（微分連鎖律）

乘法律

（微分乘法律）

除法律

（微分除法律）

導數

導數一

正弦函式的導數
假設正弦函式y=sin x（x的單位為弧度）上有一點(x,y)和另一點(x+δx,y+δy)：
d/dx(sin x)
=limδx→0 δy/δx
=limδx→0 [sin (x+δx)-sin x]/δx
=limδx→0 2[cos 0.5(2x+δx)][sin 0.5(δx)]/δx （sin A-sin B=2[cos 0.5(A+B)][sin 0.5(A-B)]）
=limδx→0 [cos 0.5(2x+δx)][sin 0.5(δx)]/0.5δx （兩邊除以2）
=limδx→0 [cos 0.5(2x+δx)]×[sin 0.5(δx)]/0.5δx
=limδx→0 [cos 0.5(2x+δx)]×limδx→0 [sin 0.5(δx)]/0.5δx
=cos 0.5(2x)×1 （limθ→0 (sin θ)/θ=1）
=cos x
最後得出d/dx(sin x)=cos x。
餘弦函式的導數
我們知道cos x=sin(π/2-x)，所以d/dx(cos x)=d/dx[sin (π/2-x)]。
假設π/2-x=u，我們可以用連鎖律對餘弦函式y=cos x求導：
d/dx(cos x)
=d/dx[sin (π/2-x)]
=d/du[sin (π/2-x)]×d/dx(π/2-x) （連鎖律）
=cos (π/2-x)×(-1) （d/dx(sin x)=cos x）
=-cos (π/2-x)
=-sin x （cos (π/2-x)=sin x）
最後得出d/dx(cos x)=-sin x。
正切函式的導數
由於正切函式tan x=(sin x)/(cos x)，我們可以用除法律對其求導：
d/dx(tan x)
=d/dx[(sin x)/(cos x)] （tan x=(sin x)/(cos x)）
=[(cos x)d/dx(sin x)-(sin x)d/dx(cos x)]/(cos^2 x) （除法律）
=[cos^2 x-(sin x)(-sin x)]/cos^2 x
=(cos^2 x+sin^2 x)/cos^2 x
=1/cos^2 x
=sec^2 x
最後得出d/dx(tan x)=sec^2 x。
三角函式的套用1
當我們遇到y=sin/cos/tan u（u是自變數為x的函式且常為ax+b的形式）這類函式的時候，可以使用連鎖律求導：
①y=sin u
d/dx(sin u)
=(dy/du)(du/dx) （連鎖律）
=(cos u)(du/dx)
當u的形式為ax+b時，du/dx=a，所以：
d/dx[sin(ax+b)]=a[cos(ax+b)]
②y=cos
當u的形式為ax+b時，du/dx=a，所以：
d/dx[cos(ax+b)]=-a[sin(ax+b)]
③y=tan u
d/dx(tan u)
=(dy/du)(du/dx) （連鎖律）
=(sec^2 u)(du/dx)
當u的形式為ax+b時，du/dx=a，所以：
d/dx[tan(ax+b)]=a[sec^2(ac+b)]
三角函式的套用2
有時我們需要對y=sin^n x或y=cos^n x（n為常數）這類函式求導，使用連鎖律也可以解決：
這裡我們使用“連鎖律的套用1”中得到的公式：d/dx(y^n)=[ny^(n-1)](dy/dx)
①y=sin^n x
dy/dx
=n[sin^(n-1) x]d/dx(sin x)
=n[sin^(n-1) x](cos x)
②y=cos^n x
dy/dx
=n[cos^(n-1) x]d/dx(cos x)
=-n[cos^(n-1) x](sin x)
得出公式：
d/dx(sin^n x)=n[sin^(n-1) x](cos x)
d/dx(cos^n x)=-n[cos^(n-1) x](sin x)

導數二

自然指數函式的導數
在畫圖軟體里，我們可以看出在函式y=e^x上任意一點(x,y)的斜率均等於y。也就是說，m=dy/dx=y。
因此，函式e^x的導數由以下公式獲得
證明：y=e^x,
y+dy=e^(x+dx),
dy=e^(x+dx)-e^x
=e^x(e^dx-1)
=e^x(1+dx+dx^2/2!+……+dx^n/n!-1){e^a=1+a+a^n/n!(n∈N）}
≈dxe^x
∴d/dx(e^x)=e^x
自然指數函式的套用
我們可以使用連鎖律對y=e^u（u是自變數為x的函式）求導：
dy/dx
=(dy/du)(du/dx) （連鎖律）
=[d/du(e^u)](du/dx)
=(e^u)(du/dx)
最後得出：
d/dx(e^u)=(e^u)(du/dx)
如果u的形式為ax+b（a和b均為常數），那么du/dx=a，可以得出：
d/dx[e^(ax+b)]=ae^(ax+b)
自然對數函式的導數
我們可以通過d/dx(e^x)=e^x對自然對數函式y=ln x求導：
y=ln x
x=e^y
d/dx(x)=d/dx(e^y)
d/dx(x)=d/dy(e^y)(dy/dx) （連鎖律）
d/dx(x)=(e^y)(dy/dx)
(e^y)(dy/dx)=1
x(dy/dx)=1 （x=e^y）
dy/dx=1/x
最後得出：
d/dx(ln x)=1/x
自然對數函式的套用
我們可以使用連鎖律對y=ln u（u是自變數為x的函式）求導：
dy/dx
=(dy/du)(du/dx) （連鎖律）
=[d/du(ln u)](du/dx)
=(1/u)(du/dx)
可以得出：
d/dx(ln u)=(1/u)(du/dx)
如果u的形式為ax+b（a和b均為常數），那么du/dx=a，可以得出：
d/dx[ln (ax+b)]=a/(ax+b)

特殊導數

三角函式
d/dx(sin x)=cos x
d/dx(cos x)=-sin x
d/dx(tan x)=sec^2 x
d/dx[sin(ax+b)]=a[cos(ax+b)]
d/dx[cos(ax+b)]=-a[sin(ax+b)]
d/dx[tan(ax+b)]=a[sec^2(ax+b)]
d/dx(sin^n x)=n[sin^(n-1) x](cos x)
d/dx(cos^n x)=-n[cos^(n-1) x](sin x)
自然指數函式
d/dx(e^x)=e^x
d/dx(e^u)=(e^u)(du/dx)
d/dx[e^(ax+b)]=ae^(ax+b)
自然對數函式
d/dx(ln x)=1/x
d/dx(ln u)=(1/u)(du/dx)
d/dx[ln (ax+b)]=a/(ax+b)

微分套用

法線
我們知道，曲線上一點的法線和那一點的切線互相垂直，微分可以求出切線的斜率，自然也可以求出法線的斜率。
假設函式y=f(x)的圖象為曲線，且曲線上有一點(x1,y1)，那么根據切線斜率的求法，就可以得出該點切線的斜率m：
m=dy/dx在(x1,y1)的值
所以該切線的方程式為：
y-y1=m(x-x1)
由於法線與切線互相垂直，法線的斜率為-1/m且它的方程式為：
y-y1=(-1/m)(x-x1)
增函式與減函式
微分是一個鑑別函式（在指定定義域內）為增函式或減函式的有效方法。
鑑別方法：dy/dx與0進行比較，dy/dx大於0時，說明dx增加為正值時，dy增加為正值，所以函式為增函式；dy/dx小於0時，說明dx增加為正值時，dy增加為負值，所以函式為減函式。
例1：分析函式y=x^2-1 的增減性
∵y=x^2-1
∴dy/dx=2x
當x>0時，dy/dx>0，所以函式y=x^2-1在x>0時是增函式；
當x<0時，dy/dx<0，所以函式y=x^2-1在x<0時是減函式。
變化的速率
微分在日常生活中的套用，就是求出非線性變化中某一時間點特定指標的變化。
比如說，有一個水箱正在加水，水箱裡水的體積V（升）和時間t（秒）的關係為V=5-2/(t+1)，
在t=3時，我們想知道此時水加入的速率，於是我們算出dV/dt=2/(t+1)^2，代入t=3後得出dV/dt=1/8。
所以我們可以得出在加水開始3秒時，水箱裡的水的體積以每秒1/8升的速率增加。

相關詞條

熱門詞條

聯絡我們