基本介紹
- 中文名:哈密頓—雅可比方程
- 外文名:Hamilton-Jacobi equation
- 領域:物理學;經典力學
- 簡稱:HJE
簡介
數學表述
各種力學表述的比較





詳解

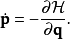


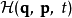


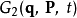
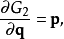


1.哈密頓主函式




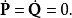



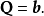
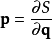


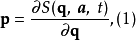




2.哈密頓特徵函式





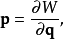

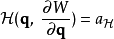





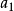

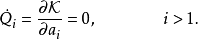









分離變數法






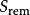





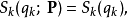
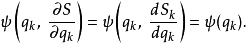









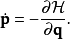


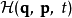


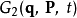
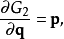






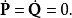



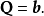
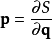


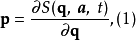






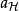

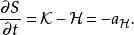

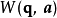

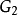
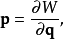

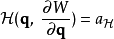





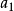

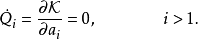















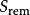





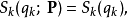
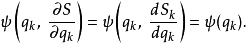



在物理學裡,哈密頓-雅可比方程 (Hamilton-Jacobi equation,HJE) 是經典力學的一種表述。哈密頓-雅可比方程、牛頓力學、拉格朗日力學、哈密頓力學,這幾個表述是互相...
哈密頓-雅可比-貝爾曼方程(Hamilton-Jacobi-Bellman equation,簡稱HJB方程)是一個偏微分方程,是最優控制的核心。HJB方程式的解是針對特定動態系統及相關代價函式下,有...
哈密頓-雅可比-貝爾曼-埃薩克斯方程(Hamil-ton-Jacobi-Bellman-Isaacs equation)微分對策問題中一種基本方程...
在廣義相對論中,哈密頓-雅可比-愛因斯坦方程(英語:Hamilton–Jacobi–Einstein equation,簡稱HJEE)是一道哈密頓形式、描述超空間中的幾何力學的方程。創於“幾何力學...
雅可比定理(Jacobi theorem)是用哈密頓-雅可比方程解哈密頓方程組的一個方法。...... 雅可比定理(Jacobi theorem)是用哈密頓-雅可比方程解哈密頓方程組的一個方法。...
哈密頓方程組(Hamilton system)是與歐拉-拉格朗日方程組等價的一階微分方程組。...... 光程函式 S滿足哈密頓-雅可比方程哈密頓方程組是變分積分或的歐拉-拉格朗日方...
他還發展了這些方程的積分理論,並用這一理論解決了力學和天文學的一些問題。值得一提的是,在表述經典力學的各種理論中唯有哈密頓-雅可比理論可用於量子力學。另外,...
經典力學中一組描寫系統運動的一階微分方程組。是W.R.哈密頓於1834年提出的,又稱哈密頓方程或正則方程。...
哈密爾頓-雅戈比方程是分析力學中用以求解正則方程的一個偏微分方程 。哈密頓-雅可比方程Hamilton-Jacobi equation由CGJ雅可比在W.R.哈密頓研究工作基礎上給出而得名...
該哈密頓量完全由動能項組成。若考慮一個黎曼流形或一個偽黎曼流形,使得存在一個可逆,非退化的度量,則該余度量可以簡單的由該度量的逆給出。哈密頓-雅可比方程...
哈密頓算符產生了量子態的時間演化。若為在時間 t 的系統狀態,其中為約化普朗克常數。此方程為薛丁格方程。(其與哈密頓-雅可比方程具有相同形式,也因為此,H 冠...
哈密頓在數學上的成就,以微分方程和泛函分析兩個領域最為突出,如哈密頓算符、哈密頓-雅可比方程等;此外,他對波形曲面的研究,對伽羅瓦理論的補充以及在數學中引入...
哈密頓一雅可比一貝爾曼一艾薩克斯條件(Hamil- ton-Jacobi-Bellman-Issacs condition)簡稱HJBI 條件。...
這樣的方程稱為一階偏微分方程的標準型,也稱為哈密頓一雅可比方程.在幾何光學中稱為光程函式方程.[1] 參考資料 1. 數學辭海第3卷 詞條標籤: 科學 ...
哈密頓向量場是經典力學中的哈密頓方程的幾何表現形式,哈密頓向量場的積分曲線...作為一個推論,泊松括弧滿足雅可比恆等式。這意味著M上可微函式組成的向量空間,...
通過特徵理論,可以看到物理光學的基本概念波前與幾何光學的基本概念光線這兩者的緊密聯繫。(見雙曲型偏微分方程、哈密頓-雅可比理論)...
哈密頓-雅可比-貝爾曼方程提供了最佳解的充份必要條件,但該條件須在整個狀態空間中都要成立。龐特里亞金最大化原理最大化和最小化 編輯 此定理一開始的名稱是龐...
廣義衝量又稱典型系統或正則系統或哈密頓典型系統(方程),常簡記為H.S.。指如下形式的一階微分方程系統 或簡寫為 是由英國科學家W.R.哈密頓於1835年引進,廣泛...
該哈密頓量完全由動能項組成。若考慮一個黎曼流形或一個偽黎曼流形,使得存在一個可逆,非退化的度量,則該余度量可以簡單的由該度量的逆給出。哈密頓-雅可比方程...
分析力學又分為拉格朗日力學或哈密頓力學。前者以拉格朗日量刻劃力學系統,運動方程...例如用分析力學知識求出漢密爾頓函式,再化成漢密爾頓算符,又自漢密爾頓-雅可比方程...
哈密頓算符產生了量子態的時間演化。若 為在時間t的系統狀態,。其中 為約化普朗克常數。此方程為薛丁格方程。(其與哈密頓-雅可比方程具有相同形式,也因為此,H冠...
2.4 哈密頓-雅可比方程2.4.1 哈密頓-雅可比方程推導2.4.2 哈密頓特徵函式2.5 作用變數和角變數2.5.1 作用變數定義2.5.2 角變數定義2.6 連續系統的哈密頓表述...
第3章是哈密頓力學,包括哈密頓正則方程、正則變換、泊松括弧以及哈密頓-雅可比方程等。第4章介紹剛體的運動學和動力學,其中後者採用拉格朗日方法來討論。第5章對非...
哈密頓認為,在零波長極限,波傳播趨向於明確的運動,但他並沒有給出一個具體方程來描述這波動行為,而薛丁格給出了這方程。他從哈密頓-雅可比方程成功地推導出薛丁格...
第3章是哈密頓力學,包括哈密頓正則方程、正則變換、泊松括弧以及哈密頓-雅可比方程等。第4章介紹剛體的運動學和動力學,其中後者採用拉格朗日方法來討論。第5章對非...
