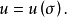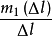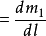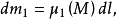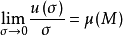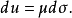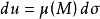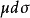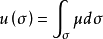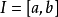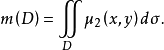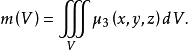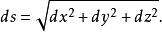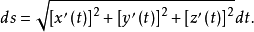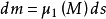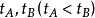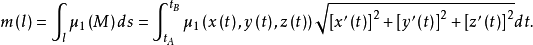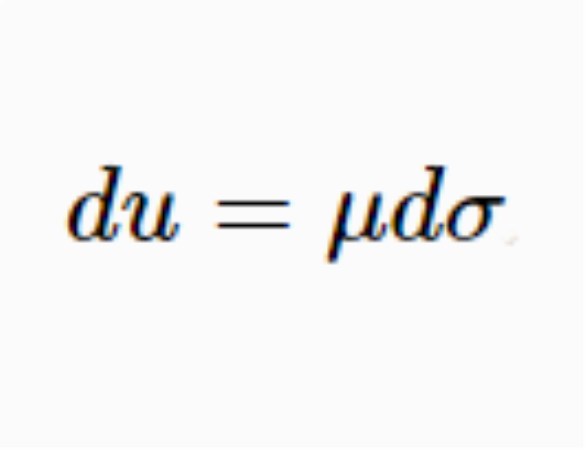區域函式(region function)是一種以區域為自變數的函式，對任意的n∈N+，若D是Rn中的區域，而對D的每個子區域D′，對應著惟一的實數，這個對應關係(法則)F就稱為定義在D上的一個區域函式。若對於D的任意兩個沒有公共內點的區域D1和D2，F還滿足F(D1∪D2)=F(D1)+F(D2)(D1∪D2仍為區域時)，則F可進一步稱為加性區域函式，n=1時，(加性)區域函式可稱為(加性)區間函式。數學分析中研究區域函式(區間函式)的意義在於，只有加性區域函式(區間函式)，才可能用重積分或定積分表示。例如，面積、體積、位移、功等都是加性區域(區間)函式，因此，它們都能用重積分或定積分來進行計算；而像平均速度、平均密度、曲邊梯形的平均高度這些物理量和幾何量，則是沒有加性的區域(區間)函式，所以，它們不可能表示成積分。在數學中，加性區域函式實質上是特殊的測度。
基本介紹
- 中文名：區域函式
- 外文名：region function
- 所屬學科：數學（高等數學）
- 所屬問題：數學分析
- 簡介：以區域為自變數的函式
基本介紹,區域函式的導數—密度函式,密度函式的積分,
基本介紹
區域函式這個概念，是人們在實踐活動中可以直接體驗到的。例如，地球上區域的面積隨著這個區域的不同而不同，又如非均勻金屬絲的質量仍隨著所取一段l的變化而變化，所以m就是l的函式，m=m(l)。
定義 一般地，若變數u隨著區域σ的變化而變化，我們就稱u是區域σ的函式，記為
區域函式的導數—密度函式
在引進二重積分時，討論從物體的密度求質量的問題，這裡要著重指出，物體的密度實際上是區域函式的某種導數，同一元函式的導數情形相似，利用極限可以從區域函式導出各種密度函式來。
例如，當我們討論非均勻細金屬絲的質量分布時，為了刻劃質量在各點的不均勻性，就要引進線密度概念。設細絲質量為m1=m1(l)，它是線段l的函式，M是金屬絲上的點，取含有點M的小段
，也用來表示這小段的長度，
就是這一段細絲的平均密度；當收縮到點M時，平均密度的極限值稱為細絲在點M的線密度，記為μ1(M)，這是從區域函式m1(l)誘導出來的點函式，也就是當收縮到點M，因而
隨著的消失而消失時所保留下來的關係。我們也記為μ1(M)
，隨之有微分公式
其中
是曲線(細絲)的弧長元素。
一般地，設σ是空間Ω的區域，u(σ)是區域σ的函式，區域的度量(長度，面積或體積)仍記為σ，將σ無限細分，使得區域σ收縮到一點M，其度量σ→0，如果
例如，當σ是三維空間中的曲面時，μ(M)就是曲面的面密度，當σ是三維空間的物體時，μ(M)就是體密度。具體寫出時，μ(M)都是x，y，z三元函式，但應該注意它們是從不同的區域函式導出的。
密度函式的積分
一元函式的微分和積分是高等數學中的一對基本矛盾，它們之間的對立統一，構成一元函式微積分學非常生動豐富的內容，這是辯證法在數學中的一個重要運用，相應地在多元函式的微積分中也是如此，上面已引進了各種區域函式的導數和微分的概念，得到區域函式u(σ)和密度函式μ(M)之間的關係：
。根據對立統一的觀點，如果將
在區域σ上重新無限累加起來，就得到積分：
。由於積分區域的不同，就有各種不同形式的積分；這些積分，無非是各種形式的區域函式罷了。下面分幾方面來敘述。
1.直線上的線密度μ1(x)和單積分
如果已知非均勻細桿的密度μ1，求細桿的質量m，就是求積分
2．平面上的面密度μ2(x,y)和二重積分
如果已知薄片的密度μ2(x,y)，求薄片的質量，就是求二重積分
3．體密度μ3(x,y,z)和三重積分
如果已知物體的密度μ3(x,y,z)，求這物體的質量，就是求三重積分
4．線密度和關於弧長元素ds的積分
空間曲線的弧長，也是由內接折線段長度之和的極限來表達，同平面曲線的情形相類似，空間曲線的弧長微分
曲線段的質量就是質量微元
的無限積累：
的積分。如果曲線的方程為，l的端點A，B所對應的參數為
，那么這個積分可按下式計算：
