基本介紹
定理信息
橢圓運算元

解析指標

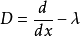







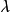
拓撲指標












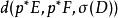
例子









發展
創立者
證明手法








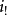
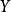

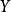







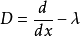







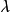












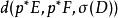


















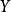

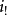



阿蒂亞-辛格指標定理(Atiyah-Singer Index Theorem)是微分幾何和拓撲學中的一個定理。此定理由英國數學家麥可·阿蒂亞與美國數學家艾沙道爾·辛格於1962年給出第一...
2004年,艾沙道爾·辛格獲得阿貝爾獎。 [3] 艾沙道爾·辛格主要成就 編輯 1962年與英國數學家麥可·阿蒂亞合作提出阿蒂亞-辛格指標定理(Atiyah-Singer Index ...
博特周期性定理是匈牙利著名數學家博特(Raoul Bott,1924.9.24-2000.12.20)證明的一個周期性定理。引入了莫爾斯-博特函式,博特-陳形式,參與了阿蒂亞-辛格指標定理...
劍橋大學三一學院 主要成就 “阿蒂亞-辛格指標定理”證明者之一 1966年獲菲爾茲獎 2004年獲阿貝爾獎 1983年被封為下級勛位爵士 目錄...
數學定理列表(按字母順序排列) 以下列出了許多數學定理,供查閱與引用。...15定理6714(黑洞數)定理A阿貝爾-魯菲尼定理阿蒂亞-辛格指標定理阿貝爾定理...
第3部分對指標定理和四維流形的性質作了較深入的探討,著重介紹了阿蒂亞-辛格指標定理如何具體套用於四種經典橢圓復形,如何套用於楊振寧-米爾斯場(Y-M場)而給出瞬...
流形上微分運算元理論是流形上的分析的一個分支,它研究流形上橢圓微分運算元及擬微分運算元的阿蒂亞-辛格指標定理及其套用。...
萊夫謝茨定理的一個重要發展是關於微分流形上橢圓型運算元與橢圓型復形的阿蒂亞-辛格指標定理與阿蒂亞-博特不動點定理。不動點理論套用 編輯 利用Brouwer不動點定理和...
陳省身推廣了高斯—波涅公式,發現了陳—高斯—波涅定理(Chern–Gauss–Bonnettheorem)。Atiyah和Singer最終又將陳—高斯—波涅定理髮展為阿蒂亞-辛格指標定理(Atiyah–...
博特(Raoul Bott,1924.9.24-2000.12.20),匈牙利著名數學家。他證明了周期性定理,引入了莫爾斯-博特函式,博特-陳形式,參與了阿蒂亞-辛格指標定理的奠基性工作,在...
麥可·法蘭西斯·阿提雅,1929年出生於英國,於1966年在莫斯科獲得菲爾茲獎,他繪出了阿提雅—辛格指標定理;為K理論的發展作出了重要貢獻;解決了李群表示論、與規範...
非常深刻的Atiyah-Singer指標定理(阿蒂亞-辛格指標定理)是Riemann-Roch定理的顛峰,Atiyah-Singer指標定理橫跨代數幾何,拓撲,分析學,偏微分方程,多複變函數論等好幾個...
此即高斯-博內(Gauss-Bonnet)定理,是更一般的阿蒂亞-辛格(Atiyah-Singer)指標定理的特例[1] 。歐拉類陳(省身)類 陳(省身)類(Chern class)是復向量叢的一種...
最後, 為緊的情形可藉阿蒂亞-辛格指標定理處理,然而,一旦取 Γ 為算術子群,便不免要處理非緊的情形。在1960年代,塞爾伯格跡公式由蘇聯的蓋爾芳特學派、普林斯頓...
M.F.阿蒂亞等人60年代初創立了微分流形上的橢圓型運算元理論。著名的阿蒂亞-辛格指標定理把運算元的解析指標與流形的示性類聯繫起來,是分析學與拓撲學結合的範例。...
劉克峰教授在微分幾何、拓撲、數學物理等研究方向取得了大量國際一流的原始創新成就,他的研究工作與阿蒂亞-辛格指標定理、費馬大定理證明這兩項二十世紀最偉大的數學...
1985年,張偉平從復旦大學數學系畢業,隨後在中國科學院數學研究所跟隨虞言林教授攻讀碩士學位。虞言林教授是當時中國首先開始從事阿蒂亞-辛格指標定理有關的研究的人。1988...
1966年 莫斯科 阿蒂亞 英國 阿蒂亞-辛格指標定理,K-理論,不動點原理 科恩 美國 連續統假設與ZF系統的獨立性 格羅騰迪克 法國 代數幾何學理論體系,泛函分析,同...
