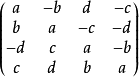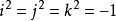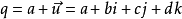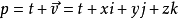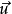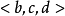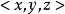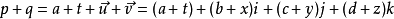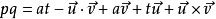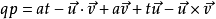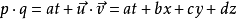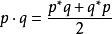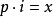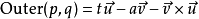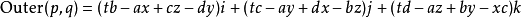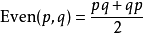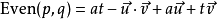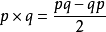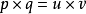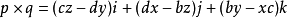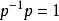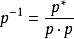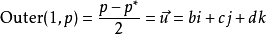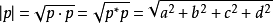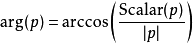四元數

四元數是簡單的超複數。 複數是由實數加上虛數單位 i 組成，其中i^2 = -1。 相似地，四元數都是由實數加上三個虛數單位 i、j、k 組成，而且它們有如下的關係： i^2 = j^2 = k^2 = -1， i^0 = j^0 = k^0 = 1 , 每個四元數都是 1、i、j 和 k 的線性組合，即是四元數一般可表示為a + bi+ cj + dk，其中a、b、c 、d是實數。

對於i、j、k本身的幾何意義可以理解為一種旋轉，其中i旋轉代表X軸與Y軸相交平面中X軸正向向Y軸正向的旋轉，j旋轉代表Z軸與X軸相交平面中Z軸正向向X軸正向的旋轉，k旋轉代表Y軸與Z軸相交平面中Y軸正向向Z軸正向的旋轉，-i、-j、-k分別代表i、j、k旋轉的反向旋轉。（見右圖）

基本介紹

• 中文名：四元數
• 外文名：Quaternions
• 發明者：愛爾蘭數學家哈密頓
• 發明時間：1843年
• 屬性：數學術語

基本信息

四元數（Quaternions）是由愛爾蘭數學家哈密頓(William Rowan Hamilton,1805-1865）在1843年發明的數學概念。四元數的乘法不符合交換律（commutative law），故它似乎破壞了科學知識中一個最基本的原則。

威廉·盧雲·哈密頓

明確地說，四元數是複數的不可交換延伸。如把四元數的集合考慮成多維實數空間的話，四元數就代表著一個四維空間，相對於複數為二維空間。

四元數是除環(除法環）的一個例子。除了沒有乘法的交換律外，除法環與域是相類的。特別地，乘法的結合律仍舊存在、非零元素仍有逆元素。

四元數形成一個在實數上的四維結合代數（事實上是除法代數），並包括複數，但不與複數組成結合代數。四元數（以及實數和複數）都只是有限維的實數結合除法代數。

四元數的不可交換性往往導致一些令人意外的結果，例如四元數的 n-階多項式能有多於 n 個不同的根。

詳見參考資料《關於四元數的幾何意義和物理套用》

基本性質

四元數就是形如 ai+bj+ck+d 的數，a、b、c、d是實數。

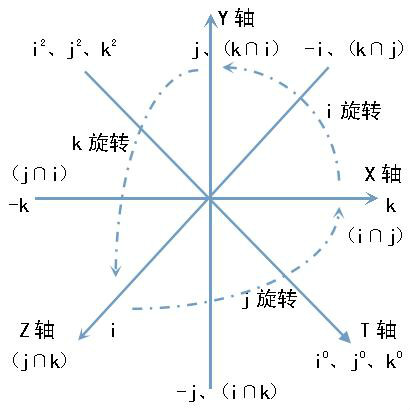
i^2=j^2=k^2=-1

ij=k、ji=-k、jk=i、kj=-i、ki=j、ik=-j

（a^2+b^2+c^2+d^2）的平方根，稱為四元數的模。

例子

假設：

x = 3 + i

y = 5i + j - 2k

那么：

x + y = 3 + 6i + j - 2k

xy =( {3 + i} )( {5i + j - 2k} ) = 15i + 3j - 6k + 5i^2 + ij - 2ik

= 15i + 3j - 6k - 5 + k + 2j = - 5 + 15i + 5j - 5k

群旋轉

像在四元數和空間轉動條目中詳細解釋的那樣，非零四元數的乘法群在R3的取實部為零的拷貝上以共軛作用可以實現轉動。單位四元數（絕對值為1的四元數）的共軛作用，若實部為cos(t)，是一個角度為2t的轉動，轉軸為虛部的方向。四元數的優點是：

非奇異表達（和例如歐拉角之類的表示相比）

比矩陣更緊湊（更快速）

單位四元數的對可以表示四維空間中的一個轉動。

所有單位四元數的集合組成一個三維球S3和在乘法下的一個群（一個李群）。S3是行列式為1的實正交3×3正交矩陣的群SO（3,R）的雙面覆蓋，因為每兩個單位四元數通過上述關係對應於一個轉動。群S3和SU（2）同構，SU（2）是行列式為1的復酉2×2矩陣的群。令A為形為a + bi + cj + dk的四元數的集合，其中a,b,c和d或者都是整數或者都是分子為奇數分母為2的有理數。集合A是一個環，並且是一個格。該環中存在24個四元數，而它們是施萊夫利符號為{3,4,3}的正二十四胞體的頂點。

矩陣表示

有兩種方法能以矩陣表示四元數，並以矩陣之加法、乘法套用於四元數之加法、乘法。

第一種是以二階複數矩陣表示。若 h = a + bi + cj + dk 則它的複數形式為：

這種表示法有如下優點：

所有複數 (c = d = 0) 就相應於一個實矩陣。

四元數的絕對值的平方就等於矩陣的行列式。

四元數的共軛值就等於矩陣的共軛轉置。

對於單位四元數 (|h| = 1）而言，這種表示方式給了四維球體和SU（2）之間的一個同型，而後者對於量子力學中的自旋的研究十分重要。（請另見泡利矩陣）

第二種則是以四階實數矩陣表示：

其中四元數的共軛等於矩陣的轉置。

歷史

四元數是由哈密頓在1843年愛爾蘭發現的。當時他正研究擴展複數到更高的維次（複數可視為平面上的點）。他不能做到三維空間的例子，但四維則造出四元數。根據哈密頓記述，他於10月16日跟他的妻子在都柏林的皇家運河（Royal Canal）上散步時突然想到 的方程解。之後哈密頓立刻將此方程刻在附近布魯穆橋（Brougham Bridge，現稱為金雀花橋 Broom Bridge）。這條方程放棄了交換律，是當時一個極端的想法（那時還未發展出向量和矩陣）。

不只如此，哈密頓還創造了向量的內外積。他亦把四元數描繪成一個有序的四重實數：一個純量（a）和向量（bi + cj + dk）的組合。若兩個純量部為零的四元數相乘，所得的純量部便是原來的兩個向量部的純量積的負值，而向量部則為向量積的值，但它們的重要性仍有待發掘。

哈密頓之後繼續推廣四元數，並出了幾本書。最後一本《四元數的原理》（Elements of Quaternions）於他死後不久出版，長達八百多頁。

用途爭辯

四元數的用途仍在爭辯之中。一些哈密頓的支持者非常反對奧利弗·亥維賽（Oliver Heaviside）的向量代數學和約西亞·威拉德·吉布斯（Josiah Willard Gibbs）的向量微積分的發展，以維持四元數的超然地位。對於三維空間這可以討論，但對於更高維四元數就失效了（但可用延伸如八元數和柯利弗德代數學）。而事實上，在二十世紀中葉的科學和工程界中，向量幾乎已完全取代四元數的位置。

詹姆斯·克拉克·麥克斯韋（James Clerk Maxwell）曾經在他的《電磁場動力理論》（A Dynamical Theory of Electromagnetic Field）直接以20條有20個變數的微分方程組來解釋電力、磁力和電磁場之間的關係。某些早期的麥克斯韋方程組使用了四元數來表述，但與後來亥維賽使用四條以向量為基礎的麥克斯韋方程組表述相比較，使用四元數的表述並沒有流行起來。

運算

綜述

四元數運算在電動力學與廣義相對論中有廣泛的套用。四元數可以用來取代張量表示。有時候採用帶有複數元素之四元數會比較容易，導得結果不為除法代數之形式。然而亦可結合共軛運算以達到相同的運算結果。

此處僅討論具有實數元素之四元數，並將以兩種形式來描述四元數。其中一種是向量與純量的結合，另一形式兩個創建量（constructor）與雙向量（bivector；i、j與k）的結合。

定義兩個四元數：

其中 表示矢量 ；而 表示矢量 。

四元數加法：p + q

跟複數、向量和矩陣一樣，兩個四元數之和需要將不同的元素加起來。

加法遵循實數和複數的所有交換律和結合律。

四元數乘法：pq

兩個四元數之間的非可換乘積通常被格拉斯曼（Hermann Grassmann）稱為積，這個積上面已經簡單介紹過，它的完整型態是︰

由於四元數乘法的非可換性，pq並不等於qp。格拉斯曼積常用在描述許多其他代數函式。qp乘積的向量部分是：

四元數點積： p · q

點積也叫做歐幾里德內積，四元數的點積等同於一個四維向量的點積。點積的值是p中每個元素的數值與q中相應元素的數值的乘積的和。這是四元數之間的可換積，並返回一個標量。

點積可以用格拉斯曼積的形式表示：

這個積對於從四元數分離出一個元素有用。例如，i項可以從p中這樣提出來：

四元數外積：Outer(p,q)

歐幾里德外積並不常用； 然而因為外積和內積的格拉斯曼積形式的相似性，它們總是一同被提及：

四元數偶積：Even(p,q)

四元數偶積也不常用，但是它也會被提到，因為它和奇積的相似性。它是純對稱的積；因此，它是完全可交換的。

叉積：p × q

四元數叉積也稱為奇積。它和向量叉積等價，並且只返回一個向量值：

四元數轉置：p−1

四元數的轉置通過 被定義。它定義在上面的定義一節，位於屬性之下（注意變數記法的差異）。其建構方式相同於復倒數（complex inverse）之構造：

一個四元數的自身點積是個純量。四元數除以一個純量等效於乘上此純量的倒數，而使四元數的每個元素皆除以此一除數。

四元數除法：p−1q

四元數的不可換性導致了 和 的不同。這意味著除非p是一個標量，否則不能使用q/p這一符號。

四元數純量部：Scalar(p)

四元數的標量部分可以用前面所述的點積來分離出來：

四元數向量部：Vector(p)

四元數的向量部分可以用外積提取出來，就象用點積分離標量那樣：

四元數模：|p|

四元數的絕對值是四元數到原點的距離。

四元數符號數：sgn(p)

一複數之符號數乃得出單位圓上，一個方向與原複數相同之複數。四元數的符號數亦產生單位四元數：

四元數輻角：arg(p)

幅角函式可找出一4-向量四元數偏離單位純量（即：1）之角度。此函式輸出一個純量角度。