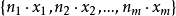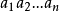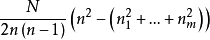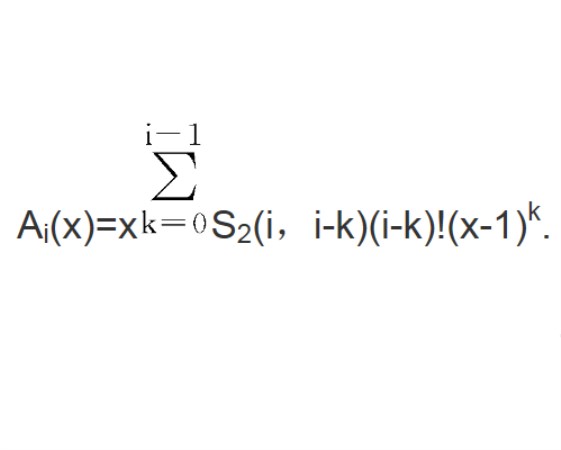西蒙-紐科姆問題

西蒙-紐科姆問題(Simon-Newcomb's problem)是確定某種排列數的一個問題，設π是多重集S={i^ki|i=1，2，…，n}的一個排列，把π分段，使得段數最少且每段中數字呈非降順序，這樣的每一段稱為π的一個上升段.所謂西蒙-紐科姆問題就是求S的恰有r個上升段的排列數N(1^k1，2^k2，…，n^kn;r).若以S₂(n，k)表第二類斯特林數，則N(1^k1，2^k2，…，n^kn;r)等於(A)^k1₁(A)^k2₂…(A)^kn_n的展開式中x^r的係數，其中的(A)_i=A(A+1-x)(A+2-2x)…·(A+k-1-(k-1)x)，Aⁱ≡A_i(x)，n=1，2，…，且A_i(x)=x∑^i-1_k=0S₂(i，i-k)(i-k)!(x-1)^k。

基本介紹

• 中文名：西蒙-紐科姆問題
• 外文名：Simon-Newcomb's problem
• 所屬學科：數學（組合學）
• 簡介：確定某種排列數的一個問題
• 提出者：西蒙·紐科姆(Simon Newcomb)

基本介紹

十九世紀著名的英國天文學家西蒙·紐科姆(Simon Newcomb)把一副撲克牌一張一張地放在桌上，只要牌的面值是以非減次序出現的，他就把它們堆成一堆，但每當待堆放的下一張牌的面值小於前者時，他就開始一個新的堆，他想要知道，在整副牌以這種方式分發完畢之後，形成給定堆數的機率。

因此，西蒙·紐科姆問題就是，求在一個多重集合的隨機排列中，路段的機率分布問題。

相關介紹

下面將推導出現於這個遊戲中的平均堆數。

首先假定有m種不同類型的牌，每種類型恰有p張。例如，通常的橋牌，如果不考慮花色時，有m=13和p=4。P.A.麥克馬洪發現了套用於這種情況的值得注意的對稱性(Combinatory Analysis1，(Cambridge，1915)，212-213]：有k+1個路段的排列個數等同於有個路段的排列個數。當p=1時，這個關係易於驗證，但對於p>1時，它是十分令人驚奇的。

顯然，沒有很簡單的對應；麥克馬洪的證明是以生成函式而不是以一種組合構造為基礎的。但福塔的對應提供了一個有用的簡化，因為它告訴我們，在具有k-1個路段的排列和其兩行表示法恰含有k個x<y的列的排列之間，有一一對應。

假設給定的多重集合是，考察其兩行表示法為

的排列，可以把這個排列和同一多重集合的另一個排列結合起來

其中。如果(1)含有形如且的k個列，則(2)含有個這樣的列，因為僅僅需要考慮y>1的情況，而且等價於。由於(1)對應於具有南k+1個路段的一個排列，而(2)對應於具有個路段的一個排列，而且由於把(1)變為(2)的變換是可逆的(它把(2)變回(1)]，麥克馬洪的對稱性條件已經建立。

由於對稱性，在一個隨機排列中路段的平均數必須是

例如，利用一副標準撲克牌，由西蒙·紐康姆的單人遊戲得到的平均堆數將是25(所以它不象是一種有吸引力的單人遊戲)。

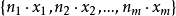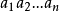給定任意多重集合，其中諸x是不同的，利用一個相當簡單的論證，實際上可以一般地確定路段的平均數。設，並想像這個多重集合的所有排列都已經寫下來，我們來考察；對於每個固定的i值，大於的機會如何，這裡1≤i<n。>的次數恰是≠的次數之半，而且不難看出，==x_j恰有次，其中N是排列的總數。因此，=恰有：

次，而且>恰有

次。因為在每個排列中定有一個路段在a_n處結束，因此若對i求和並加上N，則得到在所有N個排列當中路段的總數

除以N即給出所求的平均路段數。