基本介紹
- 中文名:線性代數
- 外文名:linear algebra
- 主要問題:線性關係問題
- 研究對象:向量、矩陣、行列式
- 套用:抽象代數、泛函分析
- 學科:數學
定義與歷史
概念
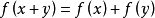
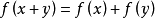
歷史
 九章算術
九章算術學術地位
基本介紹
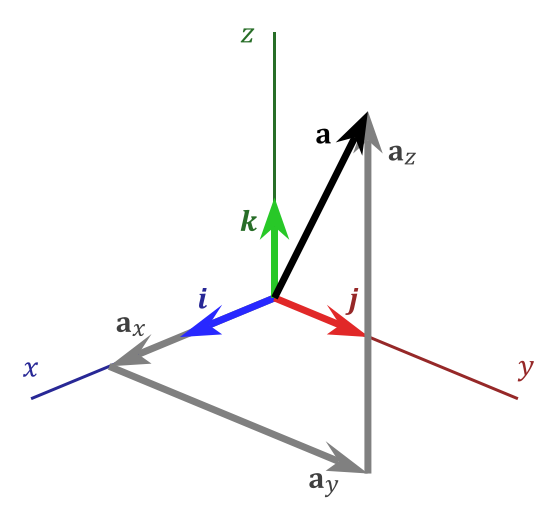 向量
向量重要定理
其他數學分支
- 模論就是將線性代數中的標量的域用環替代進行研究。
- 多線性代數將映射的“多變數”問題線性化為每個不同變數的問題,從而產生了張量的概念。
- 在運算元的光譜理論中,通過使用數學分析,可以控制無限維矩陣。

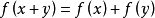
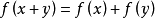
 九章算術
九章算術 向量
向量線性代數是數學的一個分支,它的研究對象是向量,向量空間(或稱線性空間),線性變換和有限維的線性方程組。向量空間是現代數學的一個重要課題;因而,線性代數被廣泛地...
《線性代數》包括行列式、矩陣、線性方程組、向量空間與線性變換、特徵值和特徵向量、矩陣的對角化,二次型及套用問題等內容。...
線性代數的理論是計算技術的基礎,同系統工程,最佳化理論及穩定性理論等有著密切聯繫,隨著計算技術的發展和計算機的普及,線性代數作為理工科的一門基礎課程日益受到重視...
書籍信息書名線性代數 書號978-7-118-09563-0 作者梁燕來、胡源艷 出版時間2014年7月 譯者 版次1版1次 開本16 裝幀平裝 出版基金 頁數138 字數221 中圖分類...
關於線性發展的歷史,計算單元為向量(組),矩陣,行列式。...... 歷史上線性代數的第一個問題是關於解線性方程組的問題,而線性方程組理論的發展又促成了作為工具的矩...
可作為普通高等學校工科、管理、財經及非數學類理科專業的教材,也可供工程技術人員或科技人員學習參考。內容主要包括行列式、矩陣、線性方程組與向量組的線性相關性、...
《線性代數》是2007年1月復旦大學出版社出版的圖書,作者是費偉勁。...... 《線性代數》是2007年1月復旦大學出版社出版的圖書,作者是費偉勁。書名 線性代數 作者 ...
本書系統地介紹了線性代數的基本理論和方法。層次清晰,論證嚴謹,聯繫實際,例題豐富。內容包括行列式、矩陣、向量空間、線性方程組、矩陣的相似對角化、二次型、線性...
《線性代數》是熊維玲在2010年出版的系統地介紹了線性代數的基本理論和方法的圖書,本書可作為高等院校工科、經管等專業的教材及教學參考書,也可供自學讀者及有關...
圖書簡介:本書包括6章內容: 行列式及其套用、矩陣、線性方程組與向量、矩陣的特徵值與特徵向量、二次型及Mathematica軟體套用·每章都配有習題,書末給出了習題答案...
在線性代數中,基(也稱為基底)是描述、刻畫向量空間的基本工具。向量空間的基是它的一個特殊的子集,基的元素稱為基向量。向量空間中任意一個元素,都可以唯一地...
《線性代數》,北京郵電大學出版社出版圖書...... 《線性代數》是根據國家教育部最新制定的本科數學基礎課程教學的基本要求和民族院校的實際情況編寫,是為適應大眾化教...
《線性代數(第五版)》是由同濟大學數學系編,高等教育出版社於2007年出版的普通高等教育“十一五”國家級規劃教材。該書可供高等院校工程類各專業使用,也可供自學...
秩是線性代數術語,在線性代數中,一個矩陣A的列秩是 A的線性無關的縱列的極大數目。類似地,行秩是 A的線性無關的橫行的極大數目。矩陣的列秩和行秩總是相等...
《工程數學線性代數》是2007年05月高等教育出版社出版的圖書,由同濟大學數學系編著。...
本書是高等職業教育工科類、管理類及經濟類基礎課教材。全書共分6章,內容包括:行列式、矩陣、向量與線性方程組、矩陣的特徵值與特徵向量、二次型及線性規劃初步。...
《線性代數》是一本由高宗升等人所編的,北京航空航天大學大學出版社出版的書籍。本書是為理工科大學(非數學專業)本科生編寫的線性代數教材。全書共分9章,主要內容...
基本信息線性代數 作者:陳小松、劉瑩、梁鑫、王宇、張夏 定價:22元 印次:1-1 ISBN:9787302480624 出版日期:2017.09.01 印刷日期:2017.08.291 內容簡介本書是...
本書共5章,內容包括線性方程組、向量空間及歐氏空間、行列式、矩陣、特徵值與特徵向量及二次型等.每節都配有習題,每章有總習題.書末給出了大部分習題的習題...
《線性代數》是2008年清華大學出版社出版的圖書,作者是鄧輝文。本書以線性方程組為主線、矩陣和向量為工具,介紹了線性代數的基本理念和基本方法,適合普通高等院校非...
本書根據教育部頒布的高等學校財經類專業核心課程“經濟數學基礎——線性代數”的教學大綱及數學和統計學指導委員會制定的《經濟管理類本科數學基礎課程教學基本要求》...
線性代數是普通高等院校理工類和經管類相關專業的一門重要基礎課。從廣義的角度看, 線性代數研究線性科學中的“線性問題”。直觀地講, 對所考慮的變數來講, 和式...
跡,是線性代數中的概念,矩陣的跡:主對角線(左上至右下的那一條)上所有元素之和。記作tr(A),其中A為方陣。...
《線性代數》是2013年8月出版的圖書,作者是寧群。...... 線性代數圖書詳細信息: 編輯 ISBN:978-7-312-03294-3 定價:22.00元 版本:1 裝幀:平裝 出版年月:...
線性代數書籍信息 編輯 作者: 譚瓊華 定價: 26 元 頁數: 178頁 ISBN: 978-7-309-07345-4/O.450 字數: 206千字 開本: 16 開 裝幀: 平裝 出版...
線性代數、高等數學 計算方法數目 兩種 套用區域 矩陣相乘、求三角形面積 目錄 1 計算方法 ▪ 直接計算——對角線法 ▪ 任何一行或一列展開——代數餘子...
奇異矩陣是線性代數的概念,就是該矩陣的秩不是滿秩。首先,看這個矩陣是不是方陣(即行數和列數相等的矩陣。若行數和列數不相等,那就談不上奇異矩陣和非奇異...
