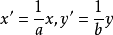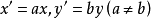相似不變數

相似不變數(similarity invariant)一般指相似變換的一種特徵，即圖形經過任何相似變換都不改變的量，例如，相似比就是最基本的相似不變數。相似不變數也指相似矩陣的相似不變數，例如相似矩陣的特徵多項式、特徵值、行列式、秩、跡。

基本介紹

• 中文名：相似不變數
• 外文名：similarity invariant
• 所屬學科：數學
• 相關概念：相似變換，相似矩陣等

相似變換的相似不變數

基本概念

關於相似群的圖形的不變性質和不變數分別稱為相似性質和相似不變數，如角度等，研究相似性質和相似不變數的幾何稱為相似幾何。

關於射影群的圖形的不變性質和不變數分別稱為射影性質和射影不變數，如同素性、結合性、交比等，研究射影性質和射影不變數的幾何稱為射影幾何。

關於仿射群的圖形的不變性質和不變數分別稱為仿射性質和仿射不變數。如平行性、分比等。研究仿射性質和仿射不變數的幾何稱為仿射幾何。

關於正交群的圖形的不變性質和不變數分別稱為度量性質和度量不變數，如距離、正交性等，研究度量性質和度量不變數的幾何稱為歐氏幾何或度量幾何。

由於射影群仿射群相似群正交群，射影幾何的研究成果適用於仿射幾何；仿射幾何的研究成果適用於相似幾何；相似幾何的研究成果適用於歐氏幾何，但反過來則不成立。因此群越大，相應的研究內容就越貧乏，但套用範圍卻越廣。 現將四種幾何的比較列表於後：

表1 四種幾何的比較

名稱	射影幾何	仿射幾何	相似幾何	歐氏幾何
變換群	射影群	仿射群	相似群	正交群
研究對象	射影性質和不變數	仿射性質和不變數	相似性質和不變數	度量性質和不變盈
基本不變性	同素性	平行性	相似性	契約性
基本不變數	交比	分比	線段之比	距離
基本不變圖形		無窮遠線	I，J	線段（長度）

例題解析

例1 下列概念中哪些是仿射的，哪些是相似而非仿射的，哪些只是度量的?為什麼?

(1)垂直；(2)線段中點；(3)中心對稱和對稱中心；(4)軸對稱；(5)三角形及其重心；(6)平行四邊形；(7)梯形；(8)二次曲線；(9)焦點、準線、離心率；(10)焦參數；(11)圓。

解： 由仿射變換保持簡比不變易知(2)是仿射概念，從而(3)也是仿射概念。

(6)、(7)是仿射概念，又因三角形、中點是仿射概念，故(5)也是仿射概念。從仿射變換的代數表示易知二次方程的代數性和次數在仿射變換下都不變，故(8)也是仿射概念。

仿射概念(2)、(3)、(5)、(6)、(7)、(8)自然也是相似概念和度量概念。

因角度、兩線段的比在相似變換下不變，故(1)、(4)是相似概念。但它們都不是仿射概念，這是因為仿射變換一般地要改變角度。

根據圓錐曲線的統一定義以及垂直性和線段比在相似變換下不變，推知(9)是相似概念，但(9)不是仿射概念，例如橢圓經仿射變換變成圓，由此易知該橢圓的焦點、準線、離心率都不是仿射不變的。

圓錐曲線過焦點且垂直於焦點所在對稱軸的弦稱為正焦弦，其長度的一半稱為焦參數，它是度量概念。但因長度在相似變換下一般要改變，故焦參數不是相似概念。

因為相似變換保持線段相等(線段比為1)不變，所以圓作為到一定點的距離相等的動點軌跡是相似概念，但圓不是仿射概念，例如直角坐標方程為的圓在仿射變換下變為橢圓。

相似矩陣的相似不變數

定義

設是定義在全體n階矩陣集合上的函式，若對中的任意兩個相似矩陣A與B，總有，則稱為相似不變數。

相關定理

定理1 矩陣的行列式是相似不變數。

證明： 設A～B，則存在可逆矩陣X，使得，於是

這說明行列式是相似不變數。

定理2 矩陣的跡是相似不變數。

證明： 顯然有

所以矩陣的跡是相似不變數。

定理3 矩陣的秩是相似不變數。

證明：因為相似矩陣是等價的，所以其秩相等。

定理4 矩陣的特徵多項式是相似不變數。

證明： 設A～B，即有可逆矩陣X使，於是

定理4說明，相似矩陣有相同的特徵多項式，因而也有相同的特徵值，故有

定理5 矩陣的特徵值是相似不變數。

順便指出，定理1～5的逆是不成立的。例如特徵多項式相同的矩陣就不一定相似。