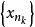基本介紹
- 中文名:波爾查諾-維爾斯特拉斯定理
- 外文名:Bolzano-Weierstrass theorem
- 別稱:緻密性定理
- 套用學科:數學
- 適用領域範圍:數學分析
定律定義,推導過程,
定律定義
緻密性定理:有界數列必有收斂子列。
先介紹子列的概念:在數列{xn}中任意抽取無限多項並保持這些項在原數列中的先後次序,這樣得到的一個數列稱為原數列的子列。
根據極限的性質,數列有界是收斂的必要條件,即如果數列收斂,那它一定有界,但反之不一定成立。可是緻密性定理卻告訴我們,只要一個數列有界,那么它一定會有收斂的子數列。
由於子列收斂,設收斂到常數A,根據極限的幾何意義,在A的ε鄰域內總有子列的無數個點。而ε是任意正數,這就意味著在A的任何鄰域內都有子列的無數個點。所以從點集的角度來描述該定理,則是:有界點集至少有一個聚點(即聚點定理)。
推導過程
緻密性定理體現了實數的連續性,與其他體現實數連續性的命題等價。特別地,聚點定理可以看做緻密性定理在點集拓撲論中的體現,或者說緻密性定理是聚點定理在實數理論中的體現,所以有的書上把這兩個定理等同來看待。
下面用實數公理——戴德金定理來證明緻密性定理。
設數列{xn}有界,即存在M>0,|xn|≤M。若{xn}中有無窮多項相等,取這無窮多項構成{xn}的一個子列,則該子列為一常數列,而常數列總是收斂的。
若{xn}中只有有限項相等,定義數集A,A中任一元素c滿足:在區間(-∞,c]上最多只有{xn}的有限項(注意用詞“最多”,這意味著(-∞,c]上可以有{xn}的0項),而區間(c,+∞)上有{xn}的無窮多項。並把A在R中的補集記為B。顯然:
①-M-1∈A,M∈B,因此A、B非空;
②A∪B=R;
③對任意p∈A,存在某個x0∈{xn},滿足p<x0。而對任意q∈B,都有x0≤q。即p<q。
根據戴德金定理,存在唯一實數ξ,要么它是A中的最大值,要么它是B中的最小值。
取任意ε>0,有ξ-ε∈A,ξ+ε∈B,因此區間(ξ-ε,ξ+ε)有{xn}的無窮多項。這是因為假設(ξ-ε,ξ+ε)只有{xn}的有限項,則根據數集A的構造,在(-∞,ξ-ε]上只有{xn}的有限項,而數列中等於ξ+ε的項最多也只有有限個,於是(-∞,ξ-ε]∪(ξ-ε,ξ+ε)∪{ξ+ε}=(-∞,ξ+ε]上只有{xn}的有限項。所以ξ+ε∈A,矛盾。
由於(-∞,ξ-ε]上只有{xn}的有限項,當ε逐漸減小時,(ξ-ε,ξ+ε)之外的項將逐漸增多。要使(ξ-ε,ξ+ε)仍有{xn}的無窮多項,則n需要足夠大,即n越大越可能留在(ξ-ε,ξ+ε)之內,n越小越可能落在(ξ-ε,ξ+ε)之外。
於是,取 ,則存在正整數
,則存在正整數 ,使
,使 ,即
,即




取 ,則存在正整數
,則存在正整數 ,使
,使 ,即
,即




……
取 ,則存在正整數
,則存在正整數 ,使
,使



這就證明了緻密性定理。