基本介紹
- 中文名:正十七邊形
- 外文名:Heptadecagon
- 類別:形狀的一種
- 適用範圍:幾何學
- 對角線:119條
- 內角和:2700°
起源
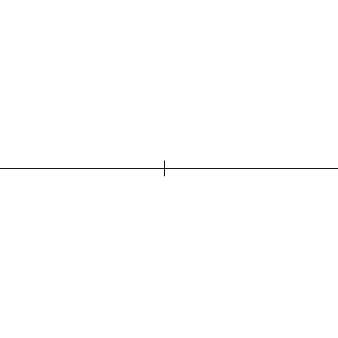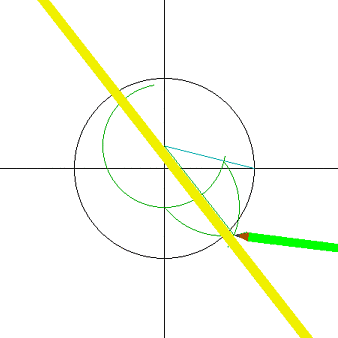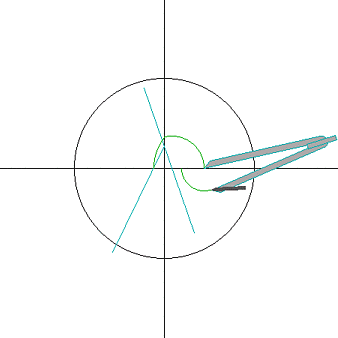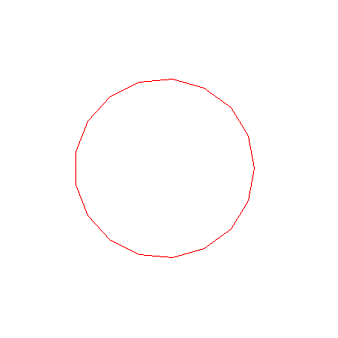
作法
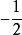

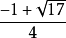

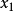
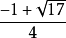

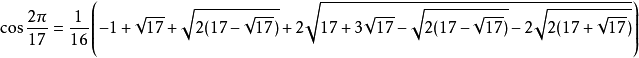
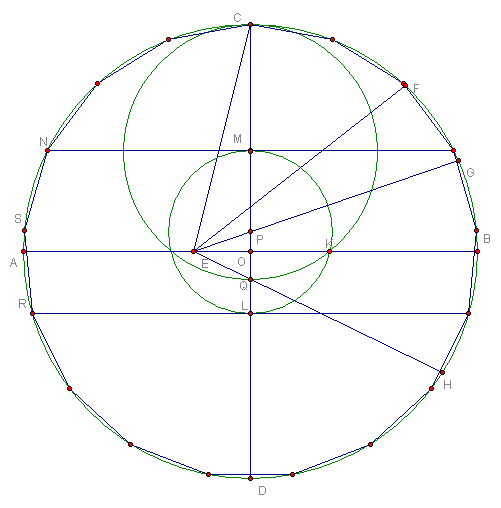
4.作∠FEB的平分線EG,交CO於P.
5.作∠GEH=45°,交CD於Q.
6.以CQ為直徑作圓,交OB於K.
7.以P為圓心,PK為半徑作圓,交CD於L、M.
8.分別過M、L作CD的垂線,交圓O於N、R.
9.作弧NR的中點S,以SN為半徑將圓O分成17等份.
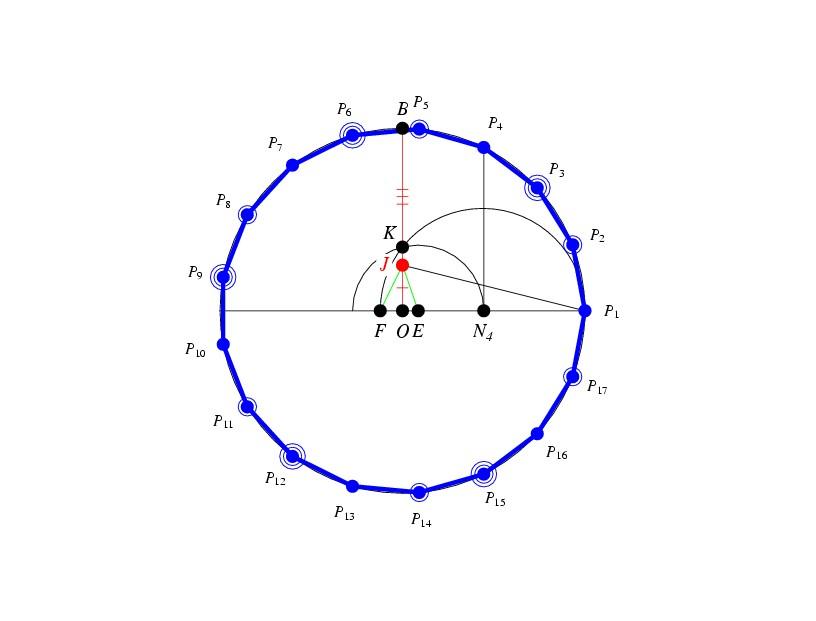
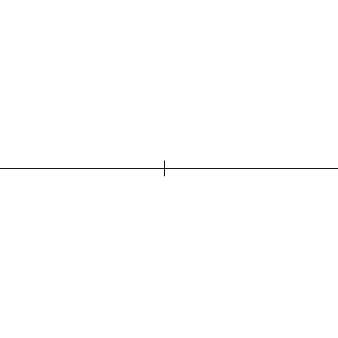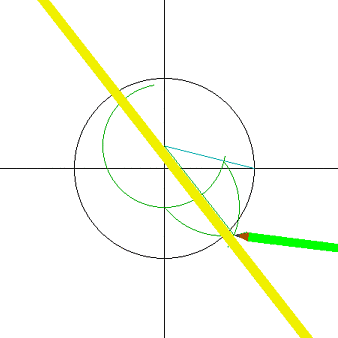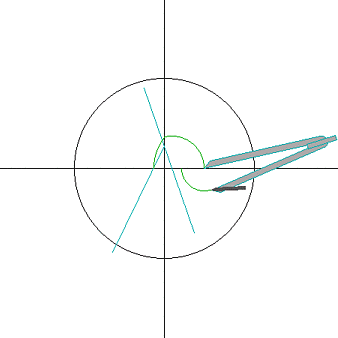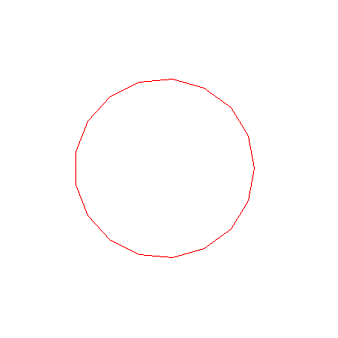

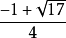

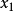
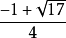

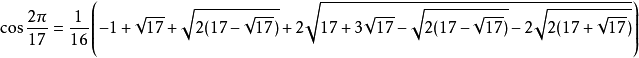

正十七邊形是指幾何學中有17條邊及17隻角的正多邊形。正十七邊形的每個內角約為158.823529411765°,其內角和為2700°,有119條對角線。最早發現其形狀可用尺規...
17(十七)是一個阿拉伯數字,介於16至18之間的一個自然數。是第7個素數(就是...1798年,高斯以尺規作圖畫出正17邊形。 連續四次方之和:1⁴+2⁴。 唯一...
《天體運動論》、《正十七邊形尺規作圖之理論與方法》 代表作品 《高等大地測量學理論(上、下)》 血型 O型 終年歲數 78歲 ...
只使用直尺和圓規,作正九邊形,此圖也不能作出來,因為單用直尺和圓規,是不足以把一個角分成三等份的。問題的解決:高斯,大學二年級時得出正十七邊形的尺規作圖...
十六、 “數學之王”高斯墓碑上的正十七邊形——正n邊形的作圖問題 十七、撲克遊戲中為什麼“同花順”最大——事件的機率計算 十八、如何估計湖中魚的數目?——...
2 3正十七邊形的作圖(10) 2 4證明(10) 2 5更簡捷的作法(11) 2 6後續(12) 3代數方程與超新星伽羅華 3 1引言(13) 3 2代數方程的求解(13) 3 3群星...
5.8 正十七邊形的構造 57本章附註 61第6章 Fermat定理及其推論 636.1 Fermat定理 636.2 二項係數的某些性質 636.3 定理72的第二個證明 656.4 定理22的...
。(所以正十七邊形可做圖)。他解決了古代三大作圖問題中的兩個:“不能任意三等分角”,“倍立方不可能”。 [2] 解讀詞條背後的知識 SME 關注科技故事 這兩...
1796年,19歲的小約翰得到了一個數學史上極重要的結果,就是《正十七邊形尺規作圖之理論與方法》。1798年轉入黑爾姆施泰特大學,翌年因證明代數基本定理獲博士學位...
4.5 合數模同餘【正十七邊形作圖法】 習題 第五章 原根與n次剩餘 5.1 指數的定義【埃及分數】 5.2 原根的存在性【阿廷猜想】 5.3 n次剩餘【佩爾...
關於質數公式的嘗試失敗了,但有意思的是,1801年數學家高斯證明:如果費馬數k為質數,那么就可以用直尺和圓規將圓周k等分.但是,高斯本人實際上並不會做正十七邊形。...
100.複數與正十七邊形[1] 參考資料 1. 高中代數妙題巧解(下冊) .豆瓣讀書[引用日期2013-02-22 20:08:39] 詞條標籤: 出版物 , 書籍 圖集...
高斯(Gauss,1777-1855)曾證明可用尺規作圖將圓周17等分,因而找到了正十七邊形的尺規作圖法。為此,後人把這一圖形銘刻在高斯紀念碑上 [1] 。...
27.3正n邊形尺規作圖的充分條件 27.4作正17邊形的高斯方法 27.5從伽羅瓦理論看正17邊形的尺規作圖 第二十八章對稱多項式的牛頓定理 28.1一個引理 28.2牛...
4.做正十七邊形。以上四個問題一直困擾數學家二千多年都不得其解,而實際上這前三大問題都已證明不可能用直尺圓規經有限步驟可解決的。第四個問題是高斯用代數...
§4.2 正多邊形4.2.1 正多邊形作圖4.2.2 同餘74.2.3 正十七邊形五 代數方程式的根§5.1 代數方程式5.1.1 一次方程與二次方程5.1.2 三次方程...
個自然數之和採用的速算法,一直被傳為佳話.1795年他進入哥廷根大學學習,第二年他就發現正十七邊形的尺規作圖法,並給出可用尺規作出正多邊形的條件,解決了...
第十三章 正十七邊形 第十四章 拔青 第十五章 金瓜子 第十六章 四級星術士 第十七章 消費 第十八章 私塾 第十九章 賄賂 第二十章 《論農業》 第二十...
當時正值十幾歲年齡段最後一年的Gauss,在是年的3月30日,發現了正十七邊形的作圖法,4月8日又證明了被Gauss自己稱為“瑰寶”的“二次剩餘互反律”(參看本書...
