基本介紹
簡介

歷史
舉例
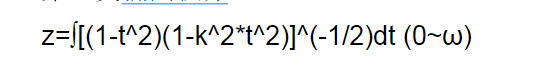
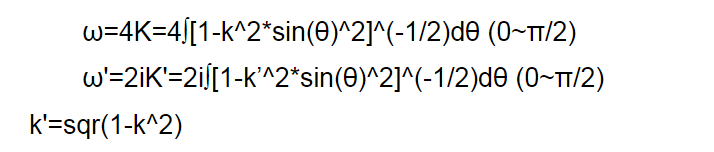
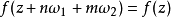

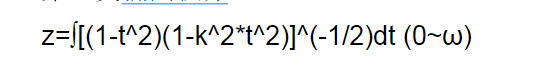
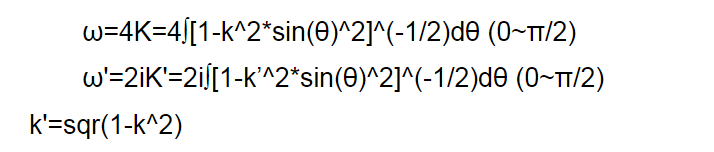
雙周期的亞純函式。它最初是從求橢圓弧長時引導出來的,所以稱為橢圓函式。橢圓函式論可以說是複變函數論在19世紀發展中最光輝的成就之一。...
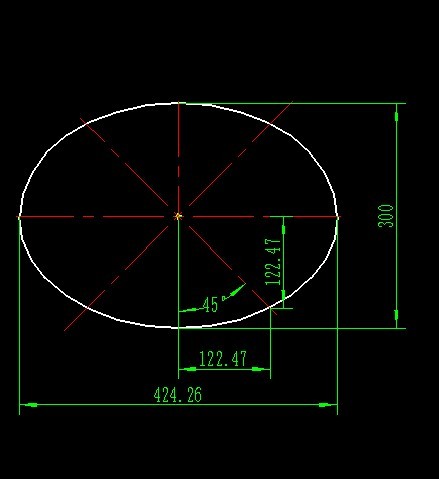
橢圓(Ellipse)是平面內到定點F1、F2的距離之和等於常數(大於|F1F2|)的動點P的軌跡,F1、F2稱為橢圓的兩個焦點。其數學表達式為:|PF1|+|PF2|=2a(2a>|F1...
第三類橢圓函式(elliptic function of the third kind )是橢圓函式(即第一類橢圓函式)的進一步推廣。橢圓函式是雙周期亞純函式的統稱。歷史上,橢圓函式是作為橢圓...
第二類橢圓函式(elliptic function of the second kind)是橢圓函式(即第一類橢圓函式)的推廣之一,另外一種為第三類橢圓函式,是橢圓函式的進一步推廣。橢圓函式是雙...
雅可比橢圓函式是雙周期的亞純函式,屬於橢圓餘弦橢圓正切,與圓函式(三角函式)相似。...
橢圓函式論新基礎(Fundamenta nova theorizefunctionum ellipticarum)西方近現代數學著作.德國數學家雅可比(Jacobi,C. G. J.)著,1829年出版.雅可比與阿貝爾(Abel ,...
《橢圓函式與模函式》是2012年10月哈爾濱工業大學出版社出版的圖書,作者是劉培傑。...... 《橢圓函式與模函式》是2012年10月哈爾濱工業大學出版社出版的圖書,作者是...
在數學中,魏爾斯特拉斯橢圓函式又稱ρ函式,是格外簡單的一類橢圓函式,也是雅可比橢圓函式的特殊形式。卡爾·魏爾斯特拉斯首先研究了這些函式。...
雅可比橢圓函式的定義第一類橢圓積分 z=∫[(1-t^2)(1-k^2*t^2)]^(-1/2)dt (0~ω) 的反函式是雙周期的亞純函式,記作 ω=sn(z)=sn(z,k) 它...
橢圓曲線是域上虧格為1的光滑射影曲線。對於特徵不等於2的域,它的仿射方程可以寫成:y^2=x^3+ax^2+bx+c。複數域上的橢圓曲線為虧格為1的黎曼面。Mordell...
橢圓濾波器(Elliptic filter)又稱考爾濾波器(Cauer filter),是在通帶和阻帶等波紋的一種濾波器。橢圓濾波器相比其他類型的濾波器,在階數相同的條件下有著最小的...
橢圓曲面就是以橢圓曲線 (虧格 的Riemann面) 為一般纖維,具有這種纖維結構的復曲面 (2維緊複流形)。...
在數論上,除數函式是一類算術函式。除數函式定義為n的正因子的次冪之和。...... 在數學中,特別是在數論中,除數函式是一...的傅立葉級數和Weierstrass橢圓函式的不...
