基本介紹
多種張量積
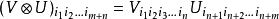
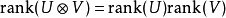
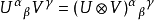
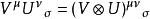
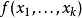
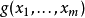
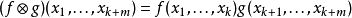
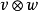
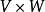
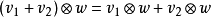
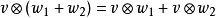
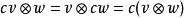
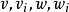
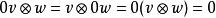
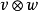
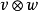

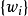

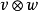
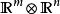
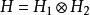
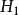
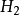
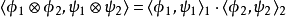
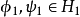
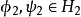
泛性質
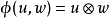
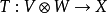
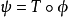
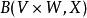
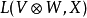
擴展
套用發展
示例
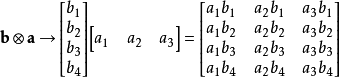

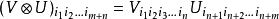
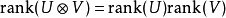
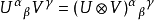
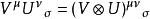
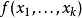
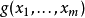
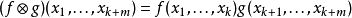
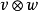
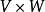
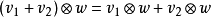
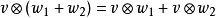
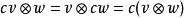
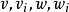
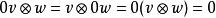
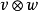
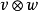

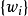

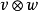
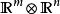
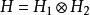
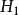
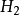
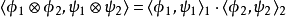
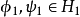
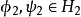
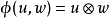
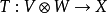
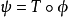
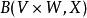
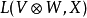
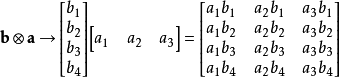
在數學中,張量積(tensor product) ,可以套用於不同的上下文中如向量、矩陣、張量、向量空間、代數、拓撲向量空間和模。在各種情況下這個符號的意義是同樣的:最一般...
,Vm的張量積空間;或簡稱P為V1,V2,…,Vm的張量積,記為: 張量空間對於多重線性代數的重要性如同向量空間對於線性代數的重要性。張量空間的維數是:...
反張量積是一種運算,八(E*,E)的第三種代數運算。...... 反張量積是一種運算,八(E*,E)的第三種代數運算。定義介紹反張量積(skew tensor product)一種運算.八...
融合張量積,簡稱融合積,是仿射李代數表示的範疇O中定義的一種張量積結構;它和頂點代數和共形場論關係密切。...
復形張量積(tensor product of complexes)模的張量積概念的推廣.設(P,a>是右A模的復形,}},(S}是左A模的復形.若Mhv `}h②w,並且定義dpq=ap⑧l。和d華...
余代數張量積是代數張量積的對偶概念。...... 余代數張量積是代數張量積的對偶概念。定義余代數張量積(tensor product of coalgebras)代數張量積的對偶概念.設(C.',4...
張量(tensor)理論是數學的一個分支學科,在力學中有重要套用。張量這一術語起源於力學,它最初是用來表示彈性介質中各點應力狀態的,後來張量理論發展成為力學和物理學...
混合張量(mixed tensor)是一類張量。向量空間及其對偶空間張量積的元素。張量是向量概念的綜合,可用以代表各向量間的關係。例如彈性張量把彈性體上每一點的變形與外...
一類由對偶空間的張量積所構成的代數。設V*,V是域K上的對偶空間,對任意的x,y∈V,x*,y*∈V*,定義 上的乘法該運算使得 成為一個非交換的結合代數,稱為V*...
的並矢積其實就是張量積。 兩個並矢積作形式上的相加就是並矢張量,從而並矢張量和二階張量(嚴格地說,是二階的反變張量)是同義詞。力學、電動力學中常見的例...
,Vm的張量積空間;或簡稱P為V1,V2,…,Vm的張量積,記為:張量空間對於多重線性代數的重要性如同向量空間對於線性代數的重要性。張量空間的維數是:...
數學上,克羅內克積是兩個任意大小的矩陣間的運算。克羅內克積是張量積的特殊形式,以德國數學家利奧波德·克羅內克命名。...
[1] 定義上描述複合系統(具有兩個以上的成員系統)之一類特殊的量子態,此量子態無法分解為成員系統各自量子態之張量積(tensor product)。 量子糾纏技術是安全的傳輸...
