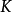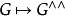基本介紹
- 中文名:對偶群
- 領域:數理科學
- 相關套用:拓撲群
定義,例子,擴展,
定義
若 是局部緊緻阿貝爾群,
是局部緊緻阿貝爾群, 的特徵標是一個從
的特徵標是一個從 到圓群
到圓群 的連續群同態;特徵標在逐點乘法下構成一個群,一個特徵標的逆元是它的復共軛。可證明所有
的連續群同態;特徵標在逐點乘法下構成一個群,一個特徵標的逆元是它的復共軛。可證明所有 上的特徵標在緊緻開拓撲(即:以緊集上的一致收斂定義收斂性)下構成一個局部緊緻阿貝爾群,稱作對偶群,記為
上的特徵標在緊緻開拓撲(即:以緊集上的一致收斂定義收斂性)下構成一個局部緊緻阿貝爾群,稱作對偶群,記為 或
或 。若
。若 可分,則
可分,則 可度量化,對一般的
可度量化,對一般的 則不盡然。
則不盡然。










定理中的自然同構定義如下:




例子
在整數對加法形成的無窮循環群 (配上離散拓撲)上,設
(配上離散拓撲)上,設 為一特徵,則
為一特徵,則 ,因此
,因此 決定於
決定於 的值;反之,給定一個,必存在特徵
的值;反之,給定一個,必存在特徵 使得
使得 ,由此得到群同構群同構
,由此得到群同構群同構 。此外也容易驗證
。此外也容易驗證 上的緊-開拓撲對應到
上的緊-開拓撲對應到 誘導自
誘導自 的拓撲。
的拓撲。











因此, 的對偶群自然地同構於
的對偶群自然地同構於 。
。


反之, 上的特徵皆形如
上的特徵皆形如 ,其中n是整數。由於
,其中n是整數。由於 是緊的,其對偶群上的拓撲由一致收斂性給出,對應的不外是
是緊的,其對偶群上的拓撲由一致收斂性給出,對應的不外是 上的離散拓撲。因此
上的離散拓撲。因此 的對偶群自然地同構於
的對偶群自然地同構於 。
。






實數對加法構成的群 同構於自身的對偶群;
同構於自身的對偶群; 上的特徵皆形如
上的特徵皆形如 ,其中
,其中 是實數。借著這些對偶性,下節描述的傅立葉變換將符應於
是實數。借著這些對偶性,下節描述的傅立葉變換將符應於 上的古典版本
上的古典版本





擴展
對偶群與對偶函子:
函子的觀點對於研究對偶群是很有用的。以下將以LCA表示所有局部緊阿貝爾群及其間的連續群同態構成之範疇。
定理:對偶函子是一個範疇等價。
定理:對偶函子的二次疊代自然同構於LCA上的恆等函子。