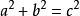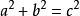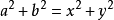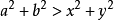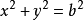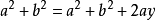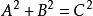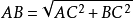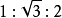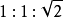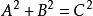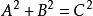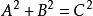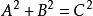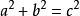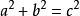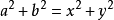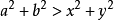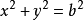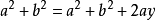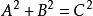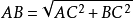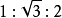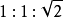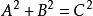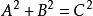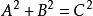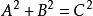內容,證法1,證法2,證法3,證法4,勾股定理,定理,勾股定理的來源,畢達哥拉斯樹,常見的勾股數,勾股弦的比例,最早套用,加菲爾德,多種證明,證法1,證法2,證法3,證法4,證法5,證法7,證法8,證法9,
內容 勾股定理 的逆定理是判斷三角形是否為
銳角 、直角或鈍角三角形的一個簡單的方法。若c為最長邊,且a
2 +b
2 =c
2 ,則△ABC是
直角三角形 。 如果a
2 +b
2 >c
2 ,則△ABC是
銳角三角形 。如果a
2 +b
2 <c
2 ,則△ABC是
鈍角三角形 。
證法1 根據
餘弦定理 ,在△ABC中,cosC=(a
2 +b
2 -c
2 )÷2ab。
由於a2 +b2 =c2 ,故cosC=0;
因為0°<∠C<180°,所以∠C=90°。(證明完畢)
證法2 證明:作AH⊥BC於H
⑴若∠C為銳角,設BH=y,AH=x
得x2 +y2 =c2 ,
(A)與(B)矛盾,∴∠C不為銳角
⑵若∠C為鈍角,設HC=y,AH=x
2ay=0
∵a≠0,∴y=0
綜上所述,∠C必為直角
證法3 已知在△ABC中,a2 +b2 =c2 ,求證△ABC是直角三角形
證明:做任意一個Rt△A'B'C',使其直角邊B'C'=a,A'C'=b,∠C'=90°。設A'B'=c'
在Rt△A'B'C'中,由勾股定理得,A'B‘2 =B'C'2 +A'C'2 =a2 +b2 =c’2
一 ∵a2 +b2 =c2 ,∴c‘=c
在△ABC和A'B'C'中,∵AB=A'B',BC=B'C',AC=A'C',∴△ABC≌△A'B'C'
∴∠C=∠C'=90°
證法4 如圖,已知在△ABC中,設AB=c,AC=b,BC=a,且a
2 +b
2 =c
2 。求證∠ACB=90°
證明:在△ABC內部作一個∠HCB=∠A,使H在AB上。
∵∠B=∠B,∠A=∠HCB
∴△ABC∽△CBH(有兩個角對應相等的兩個三角形相似)
∴AB/BC=BC/BH,即BH=a2 /c
而AH=AB-BH=c-a2 /c=(c2 -a2 )/c=b2 /c
∴AH/AC=(b2 /c)/b=b/c=AC/AB
∵∠A=∠A
∴△ACH∽△ABC(兩邊對應成比例且夾角相等的兩個三角形相似)
∴△ACH∽△CBH(相似三角形的傳遞性)
∴∠AHC=∠CHB
∵∠AHC+∠CHB=∠AHB=180°
∴∠AHC=∠CHB=90°
∴∠ACB=∠AHC=90°
勾股定理 定理 如果直角三角形兩直角邊分別為A,B,
斜邊 為C,那么
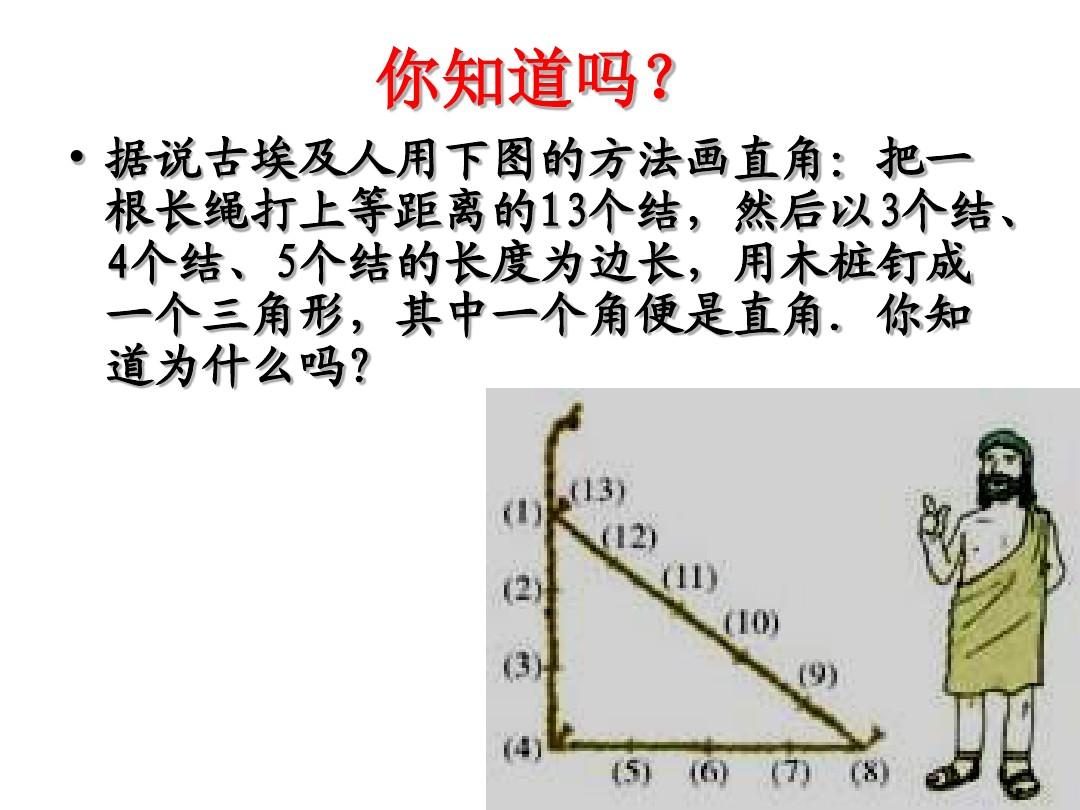
; 即直角三角形兩直角邊長的平方和等於斜邊長的平方。古埃及人用這樣的方法畫
直角 。
如果三角形的三條邊A,B,C滿足
,還有變形公式:
,如:一條直角邊是a,另一條直角邊是b,如果a的平方與b的平方和等於斜邊c的平方那么這個三角形是直角三角形。(稱勾股定理的逆定理)
勾股定理的來源 畢達哥拉斯樹 是一個基本的
幾何定理 ,傳統上認為是由古希臘的畢達哥拉斯所證明。據說畢達哥拉斯證明了這個定理後,即斬了百頭牛作慶祝,因此又稱“百牛定理”。
在中國,《
周髀算經 》記載了勾股定理的公式與
證明 ,相傳是在商代由商高發現,故又有稱之為商高定理;三國時代的
趙爽 對《周髀算經》內的勾股定理作出了詳細注釋,又給出了另外一個證明。法國和比利時稱為驢橋定理,埃及稱為埃及三角形。中國古代把直角三角形中較短的直角邊叫做勾,較長的直角邊叫做股,斜邊叫做弦。 常用
勾股數組 (3,4,5);(6,8,10);(5,12,13);(8,15,17) ;(7,24,25) 有關勾股定理書籍 《數學原理》人民教育出版社 《探究勾股定理》同濟大學出版社 《勾股書籍》 新世紀出版社 《九章算術一書》 《
幾何原本 》 (原著:
歐幾里得 )人民日報出版社
畢達哥拉斯樹 畢達哥拉斯樹是由畢達哥拉斯根據
勾股定理 所畫出來的一個可以無限重複的圖形。又因為重
複數 次後 的形狀好似一棵樹,所以被稱為畢達哥拉斯樹。 直角三角形兩個直角邊平方的和等於斜邊的平方。 兩個相鄰的小
正方形 面積的和等於相鄰的一個大正方形的面積。 利用
不等式 A2+B2≥2AB可以證明下面的結論: 三個正方形之間的三角形,其面積小於等於大正方形面積的四分之一,大於等於一個小正方形面積的二分之一
常見的勾股數 勾
股
弦
3K
4K
5K
6K
8K
10K
5K
12K
13K
7K
24K
25K
8K
15K
17K
9K
40K
41K
......
......
......
註:3K,4K,5K即3,4,5的同一
倍數 勾股數 A=s2-t2 B=2st C=s2+t2 其中s>t,且s,t為
正整數 。
勾股弦的比例 (一個銳角為30°的直角三角形)
(等腰直角三角形)
最早套用 從很多泥板記載表明,
巴比倫 人是世界上最早發現“勾股定理”的,這裡只舉一例。例如公元前1700年的一塊泥板(編號為BM85196)上第九題,大意為“有一根長為5米的木樑(AB)豎直靠在牆上,上端(A)下滑一米至D。問下端(C)離牆根(B)多遠?”他們解此題就是用了勾股定理,如圖 設AB=CD=l=5米,BC=a,AD=h=1米,則BD=l-h=5-1米=4米 ∵a=√[l2-(l-h)2]=√[52-(5-1)2]=3米,∴三角形BDC正是以3、4、5為邊的勾股三角形。《周髀算經》中勾股定理的公式與證明 《
周髀算經 》算經十書之一。約成書於公元前二世紀,原名《周髀》,它是中國最古老的天文學著作,主要闡明當時的蓋天說和四分曆法。唐初規定它為國子監明算科的教材之一,故改名《周髀算經》。 首先,《周髀算經》中明確記載了勾股定理的公式:“
若求邪至日者,以日下為勾,日高為股,勾股各自乘,並而 開方除之,得邪至日”(《周髀算經》上卷二) 而勾股定理的證明呢,就在《周髀算經》上卷一——
昔者 周公 問於商高曰:“竊聞乎大夫善數也,請問昔者包犧立周天曆度——夫天可不階而升,地不可得尺寸而度,請問數安從出?” 商高曰:“數之法出於圓方,圓出於方,方出於矩,矩出於九九八十一。故折矩,以為勾廣三,股修四,徑隅五。既方之,外半其一矩,環而共盤,得成三四五。兩矩共長二十有五,是謂積矩。故禹之所以治天下者,此數之所生也。” 周公對古代伏羲(包犧)構造周天曆度的事跡感到不可思議(天不可階而升,地不可得尺寸而度),就請教商高數學知識從何而來。於是商高以勾股定理的證明為例,解釋數學知識的由來。 《周髀算經》證明步驟
“
數之法出於圓方,圓出於方,方出於矩,矩出於九九八十一 。”:解釋發展脈絡——數之法出於圓(
圓周率 三)方(四方),圓出於方(圓形面積=外接正方形*圓周率/4),方出於矩(正方形源自兩邊相等的矩),矩出於九九八十一(長乘寬面積計算依自
九九乘法 表 )。 “
故折矩①,以為勾廣三,股修四,徑隅五。 ”:開始做圖——選擇一個 勾三(圓周率三)、股四(四方) 的矩,矩的兩條邊終點的連線應為5(徑隅五)。 “
②既方之,外半其一矩,環而共盤,得成三四五。 ”:這就是關鍵的證明過程——以矩的兩條邊畫正方形(勾方、股方),根據矩的弦外面再畫一個矩(曲尺,實際上用作直角三角),將“外半其一矩”得到的三角形剪下環繞複製形成一個大正方形,可看到其中有 邊長三勾方、邊長四股方、邊長五弦方 三個正方形。 “
兩矩共長③二十有五,是謂積矩。 ”:此為驗算——勾方、股方的面積之和,與弦方的面積二十五相等——從圖形上來看,大正方形減去四個三角形面積後為弦方,再是 大正方形 減去 右上、左下兩個長方形面積後為 勾方股方之和。因三角形為長方形面積的一半,可推出 四個三角形面積 等於 右上、左下兩個長方形面積,所以 勾方+股方=弦方。 注意: ① 矩,又稱曲尺,L型的木匠工具,由長短兩根木條組成的直角。古代“矩”指L型曲尺,“矩形”才是“矩”衍生的長方形。 ② “既方之,外半其一矩”此句有爭議。清代四庫全書版定為“既方其外半之一矩”,而之前版本多為“既方之外半其一矩”。經
陳良佐 、
李國偉 、
李繼閔 、
曲安京 等學者研究,“既方之,外半其一矩”更符合邏輯。 ③ 長指的是面積。古代對不同
維度 的量綱比較,並沒有發明新的術語,而統稱“長”。趙爽注稱:“兩矩者, 勾股各自乘之實。共長者,並實之數。 由於年代久遠,周公弦圖失傳,傳世版本只印了趙爽弦圖(造紙術在漢代才發明)。所以某些學者誤以為商高沒有證明(只是說了一段莫名其妙的話),後來趙爽才給出證明。 其實不然,摘錄趙爽注釋《
周髀算經 》時所做的《
勾股圓方圖 》——“勾股各自乘, 並之為弦實,開方除之即弦。案:弦圖
又 可以勾股相乘為朱實二, 倍之為朱實四,以勾股之差自相乘為中黃實, 加差實
亦 成弦實。” 趙爽弦圖
注意“案”中的“弦圖又 可以”、“亦 成弦實”,“又”“亦”二字表示趙爽認為勾股定理還可以用另一種方法證明,於是他給出了新的證明。 下為趙爽證明—— 青朱出入圖
三角形為直角三角形,以勾a為邊的正方形為朱方,以股b為邊的正方形為青方。以盈補虛,將朱方、青方並成弦方。依其面積關係有A2+B2=C2.由於朱方、青方各有一部分在玄方內,那一部分就不動了。 以勾為邊的的正方形為朱方,以股為邊的正方形為青方。以盈補虛,只要把圖中朱方(A2)的I移至I′,青方的Ⅱ移至Ⅱ′,Ⅲ移至Ⅲ′,則剛好拼好一個以弦為邊長的正方形(C……2).由此便可證得a2+b2=c2。
加菲爾德 1876年一個周末的傍晚,在美國首都華盛頓的郊外,有一位中年人正在散步,欣賞黃昏的美景,他就是當時美國俄亥俄州共和黨議員加
菲爾德 。他走著走著,突然發現附近的一個小石凳上,有兩個小孩正在聚精會神地談論著什麼,時而大聲爭論,時而小聲探討。由於好奇心驅使,加菲爾德循聲向兩個小孩走去,想搞清楚兩個小孩到底在乾什麼。只見一個小男孩正俯著身子用樹枝在地上畫著一個直角三角形。於是加菲爾德 便問他們在乾什麼?那個小男孩頭也不抬地說:“請問先生,如果直角三角形的兩條直角邊分別為3和4,那么斜邊長為多少呢?”加菲爾德答道:“是5呀。”小男孩又問道:“如果兩條直角邊分別為5和7,那么這個直角三角形的
斜邊 長又是多少?”加菲爾德不假思索地回答到:“那斜邊的平方一定等於5的平方加上7的平方.”小男孩說:“先生,你能說出其中的道理嗎?”加菲爾德一時語塞,無法解釋了,心裡很不是滋味。加菲爾德不再散步,立即回家,潛心探討小男孩給他出的難題。他經過反覆思考與演算,終於弄清了其中的道理,並給出了簡潔的
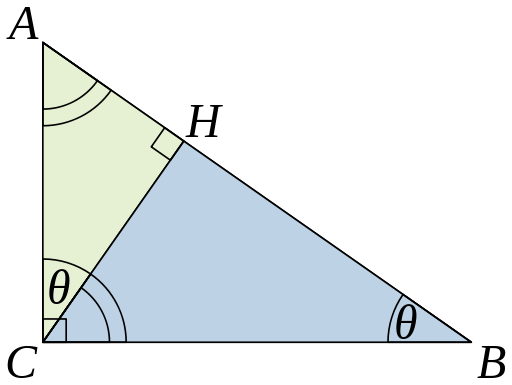
證明方法 。 如下: 解:在格線內,以兩個直角邊為邊長的小正方形面積和,等於以斜邊為邊長的正方形面積。 勾股定理的內容:直角三角形兩直角邊a、b的平方和等於斜邊c的平方, a^2+b^2=c^2
; 說明:中國古代學者把直角三角形的較短直角邊稱為“勾”,較長直角邊為“股”,斜邊稱為“弦”,所以把這個定理稱為“勾股定理”。勾股定理揭示了直角三角形邊之間的關係。 舉例:如直角三角形的兩個直角邊分別為3、4,則斜邊c的平方;= a的平方+b的平方=9+16=25即c=5 則說明斜邊為5。
多種證明 這個定理有許多證明的方法,其證明的方法可能是數學眾多定理中最多的。路明思(Elisha Scott Loomis)的
Pythagorean Proposition( 《
畢達哥拉斯 命題 》
) 一書中總共提到367種證明方式。 有人會嘗試以
三角恆等式 (例如:
正弦 和
餘弦 函式的
泰勒級數 )來證明勾股定理,但是,因為所有的基本三角恆等式都是建基於勾股定理,所以不能作為勾股定理的證明(參見
循環論證 )。
證法1 作四個
全等 的直角三角形,把它們拼成如圖那樣的一個多邊形,使D、E、F在一條直線上(設它們的兩條直角邊長分別為a、b ,斜邊長為c.)。過點C作AC的延長線交DF於點P.
∵ D、E、F在一條直線上, 且RtΔGEF ≌ RtΔEBD,
∴ ∠EGF = ∠BED,
∵ ∠EGF + ∠GEF = 90°,
∴ ∠BED + ∠GEF = 90°,
∴ ∠BEG =180°―90°= 90°
又∵ AB = BE = EG = GA = c,
∴ ABEG是一個邊長為c的正方形。
∴ ∠ABC + ∠CBE = 90°
∵ RtΔABC ≌ RtΔEBD,
∴ ∠ABC = ∠EBD.
∴ ∠EBD + ∠CBE = 90° 即 ∠CBD= 90°
又∵ ∠BDE = 90°,∠BCP = 90°, BC = BD = a.
∴ BDPC是一個邊長為a的正方形。
同理,HPFG是一個邊長為b的正方形. 設多邊形GHCBE的面積為S,則
證法2 作兩個
全等 的直角三角形,設它們的兩條直角邊長分別為a、b(b>a) ,做一個邊長為c的正方形。斜邊長為c. 再把它們拼成如圖所示的多邊形,使E、A、C三點在一條直線上. 過點Q作QP∥BC,交AC於點P. 過點B作BM⊥PQ,垂足為M;再過點 F作FN⊥PQ,垂足為N.
∵ ∠BCA = 90°,QP∥BC,
∴ ∠MPC = 90°,
∵ BM⊥PQ,
∴ ∠BMP = 90°,
∴ BCPM是一個矩形,即∠MBC = 90°。
∵ ∠QBM + ∠MBA = ∠QBA = 90°, ∠ABC + ∠MBA = ∠MBC = 90°,
∴ ∠,
又∵ ∠BMP = 90°,∠BCA = 90°,BQ = BA = c,
∴ RtΔBMQ ≌ RtΔBCA. 同理可證RtΔQNF ≌ RtΔAEF.即
證法3 作兩個全等的直角三角形,同證法2,再作一個邊長為c的正方形。把它們拼成如圖所示的多邊形. 分別以CF,AE為邊長做正方形FCJI和AEIG,
∵EF=DF-DE=b-a,EI=b,
∴FI=a,
∴G,I,J在同一直線上,
∵CJ=CF=a,CB=CD=c, ∠CJB = ∠CFD = 90°,
∴RtΔCJB ≌ RtΔCFD , 同理,RtΔABG ≌ RtΔADE,
∴RtΔCJB ≌ RtΔCFD ≌ RtΔABG ≌ RtΔADE
∴∠ABG = ∠BCJ,
∵∠BCJ +∠CBJ= 90°,
∴∠ABG +∠CBJ= 90°,
∵∠ABC= 90°,
證法4 作三個邊長分別為a、b、c的三角形,把它們拼成如圖所示形狀,使H、C、B三點在一條直線上,連結 BF、CD. 過C作CL⊥DE, 交AB於點M,交DE於點L.
∵ AF = AC,AB = AD, ∠FAB = ∠GAD,
∴ ΔFAB ≌ ΔGAD,
∵ ΔFAB的面積等於, ΔGAD的面積等於矩形ADLM 的面積的一半,
∴ 矩形ADLM的面積 =. 同理可證,矩形MLEB的面積 =.
∵ 正方形ADEB的面積 = 矩形ADLM的面積 + 矩形MLEB的面積
證法5 《幾何原本》中的證明 在歐幾里得的《幾何原本》一書中提出勾股定理由以下證明後可成立。設△
ABC 為一直角三角形,其中
A 為直角。從
A 點劃一直線至對邊,使其垂直於對邊上的正方形。此線把對邊上的正方形一分為二,其面積分別與其餘兩個正方形相等。 在正式的證明中,我們需要四個輔助定理如下: 如果兩個三角形有兩組對應邊和這兩組邊所夾的角相等,則兩三角形全等。(SAS定理) 三角形面積是任一同底同高之平行四邊形面積的一半。任意一個正方形的面積等於其二邊長的乘積。任意一個四方形的面積等於其二邊長的乘積(據輔助定理3)。證明的概念為:把上方的兩個正方形轉換成兩個同等面積的平行四邊形,再
旋轉 並轉換成下方的兩個同等面積的長方形。 其證明如下: 設△ABC為一直角三角形,其直角為CAB。其邊為BC、AB、和CA,依序繪成四方形CBDE、BAGF和ACIH。畫出過點A之BD、CE的
平行線 。此線將分別與BC和DE直角相交於K、L。分別連線CF、AD,形成兩個三角形BCF、BDA。∠CAB和∠BAG都是直角,因此C、A 和 G 都是
線性 對應的,同理可證B、A和H。∠CBD和∠FBA皆為直角,所以∠ABD等於∠FBC。因為 AB 和 BD 分別等於 FB 和 BC,所以△ABD 必須相等於△FBC。因為 A 與 K 和 L是線性對應的,所以四方形 BDLK 必須二倍面積於△ABD。因為C、A和G有共同線性,所以正方形BAGF必須二倍面積於△FBC。因此四邊形 BDLK 必須有相同的面積 BAGF = AB²;。同理可證,四邊形 CKLE 必須有相同的面積 ACIH = AC2;。把這兩個結果相加, AB2;+ AC2;; = BD×BK + KL×KC。由於BD=KL,BD×BK + KL×KC = BD(BK + KC) = BD×BC 由於CBDE是個正方形,因此AB2;+ AC2;= BC2;。此證明是於歐幾里得《幾何原本》一書第1.47節所提出的
證法6(歐幾里得(Euclid)射影定理證法)
如圖1,Rt△ABC中,∠ABC=90°,BD是斜邊AC上的高 通過證明三角形相似則有射影定理如下:
⑴(BD)2;=AD·DC,
⑵(AB)2;=AD·AC ,
⑶(BC)2;=CD·AC。 由公式⑵+⑶得:(AB)2;+(BC)2;=AD·AC+CD·AC =(AD+CD)·AC=(AC)2;, 圖1即 (AB)2;+(BC)2;=(AC)2,這就是勾股定理的結論。 圖1
證法7 在這幅“勾股圓方圖”中,以弦為邊長得到正方形ABDE是由4個相等的直角三角形再加上中間的那個小正方形組成的。每個直角三角形的面積為ab/2;中間懂得小正方形邊長為b-a,則面積為(b-a)2。於是便可得如下的式子: 4×(ab/2)+(b-a)2;=c2; 化簡後便可得:a2;+b2;=c2; 亦即:c=(a2;+b2;)1/2 勾股定理的別名 勾股定理,是幾何學中一顆光彩奪目的明珠,被稱為“幾何學的基石”,而且在
高等數學 和其他學科中也有著極為廣泛的套用。正因為這樣,世界上幾個
文明古國 都已發現並且進行了廣泛深入的研究,因此有許多名稱。 中國是發現和研究勾股定理最古老的國家之一。中國古代數學家稱直角三角形為勾股形,較短的直角邊稱為勾,另一直角邊稱為股,斜邊稱為
弦 ,所以勾股定理也稱為勾股弦定理。在公元前1000多年,據記載,商高(約公元前1120年)答周公曰“故折矩,以為句廣三,股修四,徑隅五。既方之,外半其一矩,環而共盤,得成三四五。兩矩共長二十有五,是謂積矩。”因此,勾股定理在中國又稱“商高定理”。在公元前7至6世紀一中國學者陳子,曾經給出過任意直角三角形的三邊關係即“以日下為勾,日高為股,勾、股各乘並開方除之得邪至日。 在法國和比利時,勾股定理又叫“驢橋定理”。還有的國家稱勾股定理為“平方定理”。 在陳子後一二百年,希臘的著名數學家畢達哥拉斯發現了這個定理,因此世界上許多國家都稱勾股定理為“畢達哥拉斯”定理。為了慶祝這一定理的發現,畢達哥拉斯學派殺了一百頭牛酬謝供奉神靈,因此這個定理又有人叫做“百牛定理”. 前任美國第二十屆總統
伽菲爾德 證明了勾股定理(1876年4月1日)。
1 周髀算經, 文物出版社,1980年3月, 據宋代嘉定六年本影印,1-5頁。
2. 陳良佐:周髀算經勾股定理的證明與
出入相補原理 的關係。刊於《漢學研究》, 1989年第7卷第1期,255-281頁。
3. 李國偉: 論「周髀算經」“商高曰數之法出於圓方”章。刊於《第二屆科學史研討會彙刊》, 台灣,1991年7月, 227-234頁。
4. 李繼閔:商高定理辨證。刊於《自然科學史研究》,1993年第12卷第1期,29-41頁。
5. 曲安京: 商高、趙爽與
劉徽 關於勾股定理的證明。刊於《數學傳播》20卷, 台灣,1996年9月第3期, 20-27頁
證法8 達文西的證法
證明: 第一張中多邊形ABCDEF的面積S1=S正方形ABOF+S正方形CDEO+2S△BCO=OF2+OE2+OF·OE 第三張中多邊形A'B'C'D'E'F'的面積S2=S正方形B'C'E'F'+2△C'D'E'=E'F'2+C'D'·D'E' 因為S1=S2
所以OF2+OE2+OF·OE=E'F'2+C'D'·D'E'
又因為C'D'=CD=OE,D'E'=AF=OF
所以OF2+OE2=E'F'2
因為E'F'=EF
所以OF2+OE2=EF2 勾股定理得證。
證法9 從這張圖可以得到一個矩形和三個三角形,推導公式如下:
b (a + b)= 1/2c2; + ab + 1/2(b + a)(b - a) 矩形面積 =(中間三角形)+(下方)2個直角三角形+(上方)1個直 角三角形。 (簡化) 2ab + 2b2;= c2; + b2;- a2;+ 2ab 2b2; - b2;+ a2;= c2; a2; + b2;= c2;
註:根據加菲爾德圖進一步得到的圖形。