基本介紹
- 中文名:仿射不變數
- 外文名:affine invariant
- 所屬學科:數學
- 所屬問題:高等幾何(仿射幾何)
- 簡介:圖形經過仿射變換不改變的量
- 別稱:圖形的仿射性質
基本介紹










相關定理和推論
典型例題分析

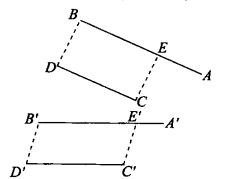 圖1
圖1



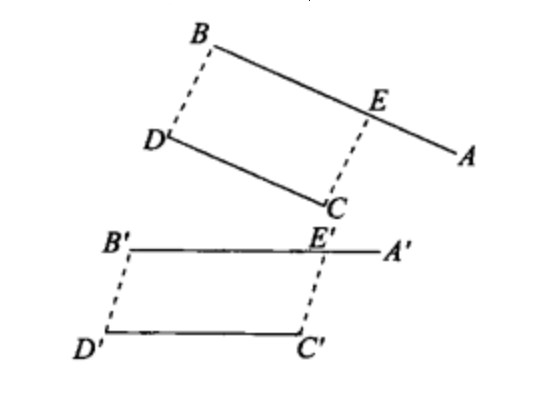











 圖1
圖1



仿射不變數(affine invariant)是仿射變換的一種特徵,指圖形經過任何仿射對應(變換)都不改變的量。共線三點的單比是最基本、最重要的仿射不變數,其他如兩平行的有...
研究圖形在仿射變換群下的不變性質和不變數的幾何學叫做仿射幾何學。在仿射幾何里,沒有角度及線段長度的概念,沒有兩個不平行錢段的比的概念,沒有面積的概念,...
歐氏變換除具有仿射不變性外還保持兩條直線的夾角不變,任意兩點的距離不變。這些不變數都是由一些幾何元素的參數計算出來的量,如由點的坐標計算出兩點的距離等。...
《模式識別中的矩和矩不變數》是2014年12月中國科學技術大學出版社出版的圖書,作者是(捷克)Jan Flusser、 (捷克)Tomas Suk、(捷克) Barbara Zitova ,譯者是...
仿射變換全體構成的變換群稱為仿射變換群。仿射變換下重要的不變性質和不變數有:共線性、平行性、平行線段的長度比等。如果在仿射平面(或空間)中引入無窮遠點,...
其他仿射不變數都可以用單比表示。在仿射平面(空間)中,仿射變換的全體構成一個變換群,稱為仿射變換群,簡稱仿射群。並且在擴大的仿射平面(空間)中,它還是保持無窮...
相似不變數(similarity invariant)一般指相似變換的一種特徵,即圖形經過任何相似變換都不改變的量,例如,相似比就是最基本的相似不變數。相似不變數也指相似矩陣的...
仿射主曲率(affine principal curvature)刻畫仿射空間中超曲面彎曲程度的不變數.它是歐氏曲面論中主曲率的仿射類似.設M是n+1維仿射空間中的局部嚴格凸的超曲面,二...
中心仿射變換(central affine transformation)是一類重要的仿射變換,指含一個不變點的仿射變換。位似變換是中心仿射變換的特例。...
仿射球面(affine hypersurface)是一個重要的超曲面,指仿射空間中仿射法線交於一點或互相平行非退化的超曲面。一個局部嚴格凸的仿射球稱為虛的或拋物型的仿射球面,...
因為在仿射變換中簡比是不變數,所以笛卡爾坐標的仿射變換就是這個等式的推廣,因為各軸的度量單位是不同的。在仿射變換中,新得到的坐標系仍是仿射坐標系 [2] 。...
按照變換群的觀點,幾何學可以這樣分類:研究射影變換群、仿射變換群、相似變換群、正交變換群下不變性質和不變數的幾何學分別是射影幾何學、仿射幾何學、拋物幾何學...
由於我們可以將二相交直線投影成二平行直線,所以二直線的平行性也不是射影性質。另外,重要的仿射不變數單比也不是射影不變數,對此可由以下例題說明:...
《得到仿射空間中很多曲面的仿射不變數》;《數學雜誌》 目錄 1 個人簡介 2 求學簡歷 3 求學花絮 4 工作經歷 5 曾任職務 6 教學方法 7 個人影響 ...
單比在數學中有兩個解釋,一個是指算術中的比,指比的前項和後項都只有一個數的比,如,5:2,8:9,是相對於複比而言的。另一個是指仿射幾何中最基本的不...
6. 賈棋,樊鑫,羅鐘鉉,田曉宇,劉宇,一種基於仿射不變數的符號識別方法,專利號:201310071948,公開(公告)號:CN103258200A。 [5] ...
仿射變換是射影變換的特殊情況,當定義中心射影的線束為互相平行的直線時,變換稱為仿射變換,由於線束中的直線互相平行,顯然,仿射變換保持交比不變。[2] ...
從視覺不變數入手,廣泛整理了現有的基於仿射近似模型的算法,在充分仿真基礎上發現,基於區域的仿射矩不變數對噪聲敏感,而基於目標輪廓的一系列仿射不變數在輪廓提取...
(7) VarBIFT:指令級的變數冗餘容錯檢測技術,計算機工程與設計,2010,第3作者(8) 指令級的變數容錯恢復,計算機工程,2010,第2作者(9) 一種基於頻域特徵的仿射不...
因為仿射幾何的群是射影幾何的群的子群,所有射影幾何的概念不變數先驗的在仿射幾何中有意義;但是反過來不行。如果你包含更多對稱性進來,你就有一個更強的理論,...
