基本介紹
- 中文名:射影性質
- 外文名:projective properties
- 定義:圖形經任何射影變換都不變的性質
- 舉例:非調和比、同素性、結合性等
- 重要著作:《論圖形的射影性質》
- 著名人物:龐斯列
相關研究

基本介紹
透視對應










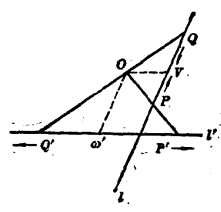 圖1
圖1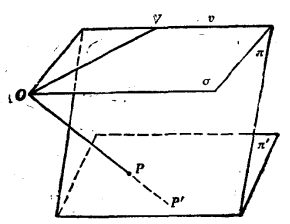 圖2
圖2射影性質舉例





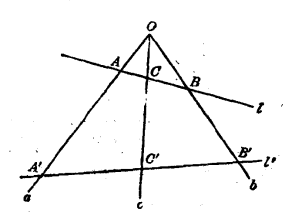 圖3
圖3


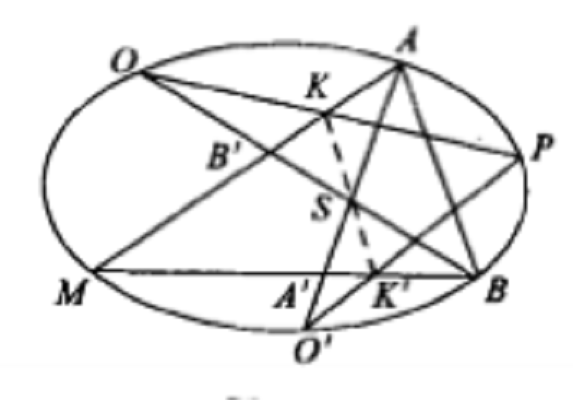











 圖1
圖1 圖2
圖2




 圖3
圖3


射影性質是射影變換的一種特徵,指圖形經過任何射影對應(變換)都不變的性質,例如,非調和比、二次曲線極點與極線的關係、一條代數曲線的類型或階、同素性、結合...
射影是一個存在於數學及物理學中的概念,存在於集合論、線性代數、幾何學以及拓撲學等諸多理念中。在平面幾何中,與一個圖形相似的圖形叫做這個圖形的射影。射影是...
論圖形的射影性質(Traite des proprietes pro-jectives des figures)是西方近現代數學著作.法國數學家、力學家彭賽列(Poncelet, J. - V.)著,1822年出版的書籍...
射影幾何是研究圖形的射影性質,即它們經過射影變換後,依然保持不變的圖形性質的幾何學分支學科。射影幾何學也叫做投影幾何學。在經典幾何學中,射影幾何處於一種...
射影平面就是2維射影空間。它可以視為平面添上一條無窮遠直線。 它是代數幾何、射影幾何里最基本的對象。對射影平面的理解是從局部到整體的擴展過程。先從無窮...
在歐幾里得直線上添加一個無窮遠點後,所得的直線稱為擴大直線或仿射直線。若在擴大直線上,對無窮遠點和有窮點不加區別,同等看待,則稱這樣的擴大直線為射影直線,...
定義1.如圖,已知∠AOB∈(0,π),設A,O,B在平面α上的射影分別為A′,O′,B′,且A′,O′,B′不共線,則稱∠A′O′B′是∠AOB在平面α上的射影角(...
由有限次中心射影的積定義的兩條直線間的一一對應變換稱為一維射影變換。由有限次中心射影的積定義的兩個平面之間的一一對應變換稱為二維射影變換。因為正交變換...
射影距離(projective distance)是射影幾何的一個術語,指射影幾何中所定義的兩點之間的距離。例如在射影平面上取定一個非退化的二階曲線,若取一個常數k(k≠0)...
射影幾何亦稱投影幾何。幾何學的一個分支。主要研究圖形在射影對應(射影變換)下不變的幾何性質。射影變換是射影幾何中最重要的幾何變換。這種變換的主要特點是...
一維射影對應(one-dimensional projective correspondence)是透視對應的推廣,兩個一維基本形(點列或線束)間的一一對應是射影對應的充分必要條件是任何四元素的交比...
射影角度(projective angular measure)是射影幾何的一個術語,指射影幾何中所定義的兩條直線的夾角。例如,在射影平面上取定一個非退化的二級曲線,另選定一個常數...
有限射影平面(finite projective plane)一類組合構形,指二維有限射影空間。...... 射影平面由一組線、一組點,以及一個點與線之間的重合關係所組成,並具有以下性...
射影幾何是研究圖形的射影性質,即它們經過射影變換後,依然保持不變的圖形性質的幾何學分支學科。也叫投影幾何學,在經典幾何學中,射影幾何處於一個特殊的地位,...
Pn(C)的一個子集,若它可以表示為定義在Cn+1中一組齊次多項式公共零點的集合,則稱它為射影代數簇,簡稱代數簇,也可稱它為Pn(C)的代數子集。...
一維射影變換(one-dimensional projective transformation)是指重疊一維基本形之間的射影對應。如果平面上兩個同類的一維基本形(同為點列或線束)是同底的或同心的,...
性質 典型群 定義 一般線性群對中心的商群 相似群 正交群、酉群、辛群 目錄...若V是K上n維右向量空間,P(V)是V的全體一維子空間的集合(即射影空間),則...
射影決定性公理(the axiom of projective de-terminacy)簡稱PD.決定性公理的一種最重要的弱形式.決定性公理認為,對任何Ac},w,對弈G(A)都是決定的,這一假定...
《圓錐曲線的幾何性質》採用綜合法,從圖形到圖形,以平面幾何知識為主,立體幾何知識為輔,介紹了圓錐曲線的大批幾何性質。主要內容包括:拋物線、正射影、橢圓、雙...
