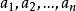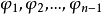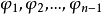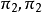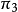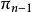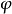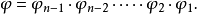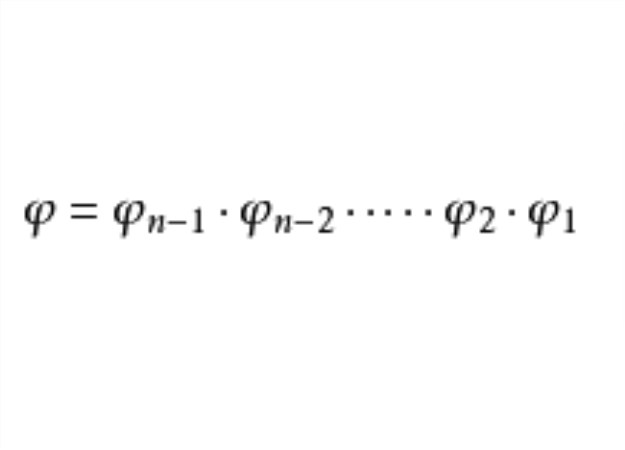仿射對應(affine correspondence)是一種重要的幾何對應，是有限個透視仿射對應的乘積。例如，設有n+1個平面α，α1，α2，…，αn-1，β。如果在平面偶(α，α1)，…，(αi，αi+1)，…，(αn-1，β)之間都存在著透視仿射對應，即每兩個相鄰平面之間都存在著平行投影，則平面α與平面β的點之間就建立起一個一一對應關係，這種對應就稱為平面α到平面β的仿射對應。仿射對應保持同素性，結合性，平行性(即互相平行的直線對應著互相平行的直線)和共線三點的單比不變。
基本介紹
- 中文名：仿射對應
- 外文名：affine correspondence
- 所屬學科：數學
- 所屬問題：高等幾何(仿射幾何)
- 簡介：有限個透視仿射對應的乘積
基本概念,二直線間的仿射對應,二平面間的仿射對應,仿射對應的性質,仿射變換的等價定義,
基本概念
把直線(平面)上的點經過平行投影到另一直線(平面)上，這樣得到的點與點間的對應稱為“平行透視”。把一個圖形經過有限次平行透視後變成另一個圖形時，叫作“仿射對應”。由一回的平行投影所成的仿射對應，又稱為“透視仿射對應”。把同一平面內單方面的透視仿射對應，稱為透視仿射變換。有限回的透視仿射變換組成仿射變換。仿射變換的主要性質有：
1．二直線的平行性是仿射變換的不變性質。
2．三點的簡比是仿射變換的不變數。
3．兩條平行線段之比是仿射變換的不變數。因此，平行四邊形是仿射變換的不變圖形(平行四邊形在仿射變換下變成平行四邊形)。
4．任意兩個三角形面積之比是仿射變換的不變數。
5．所有仿射變換構成一個群，叫作仿射變換群。
研究圖形在仿射變換群下的不變性質和不變數的幾何學叫做仿射幾何學。
在仿射幾何里，沒有角度及線段長度的概念，沒有兩個不平行錢段的比的概念，沒有面積的概念，因為這些量都不是仿射變換群的不變數，平行線段之比及面積之比是仿射變換群的不變數，所以在仿射幾何里可以討論這些概念。
二直線間的仿射對應
設同一平面內有n條直線
，用
順次表示
到
到
，……，
到
的透視仿射對應。經過這一串透視仿射對應，使上的點與
上的點建立了一一對應，這個對應稱為到的仿射對應，用
表示，於是有
如果直線與重合，則到的仿射對應叫做直線到自身的仿射變換。
二平面間的仿射對應
當與重合時，稱為l到自身的仿射變換。
仿射對應的性質
仿射對應的性質：
(1)保持同素性；即將點對應成電點，直線對應成直線。
(2)保持結合性；即保持點和直線的結合關係。
(3)保持單比不變。
(4)保持直線的平行性。
仿射變換的等價定義
若兩個平面問(平面到自身)的一個點對應(變換)保持同素性，結合性和共線三點的單比不變，則這個點對應(變換)稱為仿射對應(變換)。
陸詩榮，周慧波，呂學琴主編,高等幾何精講與精析,哈爾濱地圖出版社,2007.03,第18頁
陸詩榮，周慧波，呂學琴主編,高等幾何精講與精析,哈爾濱地圖出版社,2007.03,第17頁
