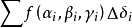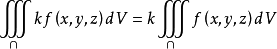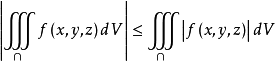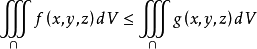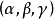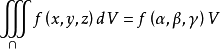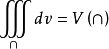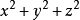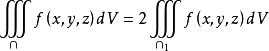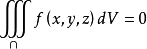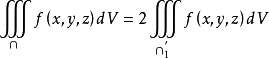定義
設三元函式z=f(x,y,z)定義在有界閉區域Ω上將區域Ω任意分成n個子域Δv
i(i=123…,n)並以Δv
i表示第i個子域的體積.在Δv
i上任取一點
作和
.如果當各個子域的直徑中的最大值λ趨於零時,此和式的
極限存在,則稱此極限為函式f(x,y,z)在區域Ω上的三重積分,記為
,即
,其中dv叫做體積元素。
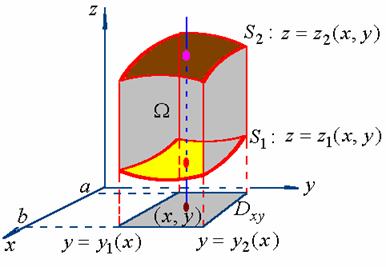 三重積分圖示
三重積分圖示其中,∫∫∫稱為三重積分號,f(x,y,z)為被積函式,f(x,y,z)dv稱為被積表達式,dv稱為體積元,x、y、z為積分變數,Ω為積分區域,
為積分和。
性質
線性性質
(1)
(k為常數),被積常數中的常數因子可以提到三重積分號外面。
(2)設α、β為常數,則
,函式的和(或差)的三重積分等於各個函式的三重積分的和或差。
可加性質
如果
空間閉區域G被有限個曲面分為有限個子閉區域,則在G上的三重積分等於各部分閉區域上三重積分的和。
不等性質
如果在G上,
f(x,y,z)≤φ(x,y,z),則有,特殊地,若函式f(x,y,z)在Ω上可積,則|f(x,y,z)|亦在Ω上可積
,且有。 估值性質
設M、m分別為f(x,y,z)在閉區域G上的
最大值和
最小值,V為G的體積,則有
mV≤≤MV。積分中值定理
設函式f(x,y,z)在閉區域G上連續,V是G的體積,則在G上至少存在一個點
使得
另外由重積分的性質知,當f(M)=1時,三重積分
,這裡V(Ω)表示空間域Ω的
度量,即V(Ω)表示Ω的體積。
計算方法
直角坐標系法
適用於被積區域Ω不含圓形的區域,且要注意積分表達式的
轉換和積分上下限的表示方法
⑴先一後二法投影法,先計算豎直方向上的一豎條積分,再計算底面的積分。
①區域條件:對積分區域Ω無限制;
②函式條件:對f(x,y,z)無限制。
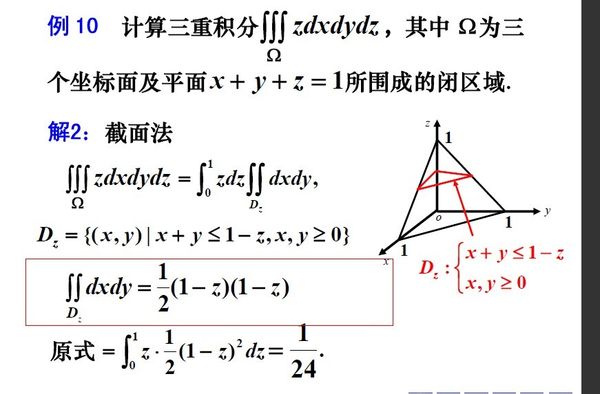
⑵先二後一法(截面法):先計算底面積分,再計算豎直方向上的積分。
①區域條件:積分區域Ω為平面或其它曲面(不包括圓柱面、圓錐面、球面)所圍成
②函式條件:f(x,y)僅為一個變數的函式。
柱面坐標法
①區域條件:積分區域Ω為圓柱形、圓錐形、球形或它們的組合;
②函式條件:f(x,y,z)為含有與
(或另兩種形式)相關的項。
球面坐標系法
適用於被積區域Ω包含球的一部分。
①區域條件:積分區域為球形或球形的一部分,錐面也可以;
幾何意義
三重積分就是立體的質量。
當積分函式為1時,就是其密度分布均勻且為1,質量就等於其體積值。
當積分函式不為1時,說明密度分布不均勻。
套用
設Ω為空間有界閉區域,f(x,y,z)在Ω上連續
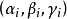
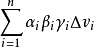
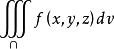

 三重積分圖示
三重積分圖示