基本介紹
- 中文名:霍普夫代數
- 外文名:Hopf algebra
- 本質:一類雙代數
定義

例子







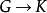







李群的上同調














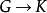










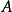


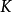
在數學中,霍普夫代數是一類雙代數,亦即具有相容的結合代數與余代數結構的向量空間,配上一個對極映射,後者推廣了群上的逆元運算。霍普夫代數以數學家海因茨·霍普夫...
霍普夫代數是20世紀60年代以後迅速發展起來的代數學的新學科。域k上的霍普夫代數是同時具有k代數結構和它的對偶結構(k余代數結構)並滿足一定的相容條件的代數系統。...
定義 商霍普夫代數(quotient Hopf algebra)商代數概念的引申.設H是一個霍普夫代數,1是H的一個霍普夫理想.H/1有惟一的霍普夫代數結構使自然同態H}H/I成為霍普夫...
對偶雙代數(dual bialgebra)是由給定雙代數誘導出的一個具雙重對偶性的雙代數。...... s,則雙代數H。有對極s0,從而成為一個霍普夫代數,稱為H的對偶霍普夫代數....
定義 霍普夫理想(Hopf ideal)對極作用下閉合的雙理想.設H是一個霍普夫代數,S是它的對極.若H的雙理想J,使得S(J)}J,則J稱為H的霍普夫理想. ...
廣霍普夫代數、半霍普夫代數、德林費爾德扭 目錄 1 人物生平 2 研究領域 3 個人影響 4 所獲獎項 弗拉基米爾·德林費爾德人物生平 編輯 弗拉基米爾·格爾紹諾維...
4一般群分次理論與霍普夫代數、馮·諾伊曼代數等理論有著深刻的聯繫。值得一提的是,分次環的理論固然重要,而更重要的是分次環的研究方法,這一點可以從分次環的...
他又推廣霍普夫代數成 半霍普夫代數, 引進了德林費爾德扭一概念,其套用包括分解對應於半三角霍普夫代數之楊-巴克斯特方程解的 R矩陣。 1990年德林費爾德獲得了一枚...
H空間的重要性質是:若(X,e)是H空間,則同調群H*(X)是具有單位元的分次代數,並且H*(X)和H(X)是對偶霍普夫代數。H空間的概念是霍普夫(Hopf,H.)於1941年...
德林斐特量子對(Drinfeld quantum double、Drinfeld double或quantum double)是數學家德林斐特於1986年柏克萊國際數學家大會上提出的一種代數結構,由有限維霍普夫代數A ...
