基本介紹
- 中文名:雙邊拉普拉斯變換
- 外文名:Bilateral Laplasse Transform
- 提出者:拉普拉斯(Pierre-Simon Laplace)
- 提出時間:1778年
- 套用學科:信號處理,通信控制
定義


優點
- 信號不必限制在範圍t>0內,在某些情況下把所研究的問題從時間負無窮到正無窮上作統一考慮,可使概念更清楚。
與傅氏變換的關係


性質




























雙邊拉普拉斯變換是一種積分變換,作用對象是任意實數t的實數函式或是複變函數 f(t),作用結果是F(s),其形式類似機率中的動差生成函式,雙邊拉普拉斯變換和傅立葉...
雙側拉普拉斯變換(bilateral Laplace transformation)是一種積分變換,作用對象是任意實數t的實數函式或是複變函數 f(t),作用結果是F(s),其形式類似機率中的動差...
Mellin 變換是一種以冪函式為核的積分變換。Mellin 變換有許多套用,例如可以證明黎曼ζ函式的函式方程。在數學中,梅林變換是一種積分變換,可以被視為雙邊拉普拉斯...
其中F表示的是傅立葉變換。這一定理對拉普拉斯變換、雙邊拉普拉斯變換、Z變換、Mellin變換和Hartley變換(參見Mellin inversion theorem)等各種傅立葉變換的變體同樣成立...
1.4.1 雙邊z變換101.4.2 雙邊拉普拉斯變換131.5 連續時間信號的離散時間處理141.5.1 CT信號的DT處理過程的基本結構141.5.2 DT濾波以及全局CT回響15...
一、微分方程的變換解二、系統函式三、系統的s域框圖四、電路的s域模型五、拉普拉斯變換與傅立葉變換5.5雙邊拉普拉斯變換習題五第六章 離散系統的z域分析...
5.8.3 雙邊拉普拉斯變換和雙邊z變換收斂域的性質5.8.4 反拉普拉斯變換和反z變換5.9 信號的復頻譜和LTI系統的系統函式習題第6章 變換的性質及其揭示的時域與頻域和...
五、拉普拉斯變換與傅立葉變換§5.5雙邊拉普拉斯變換習題五第六章 離散系統的z域分析§6.1 z變換一、從拉普拉斯變換到z變換二、z變換...
4.12 雙邊拉普拉斯變換4.13 拉普拉斯變換與傅立葉變換的關係習題第五章 傅立葉變換套用於通信系統——濾波、調製與抽樣5.1 引言5.2 利用系統函式H(jw)求回響...
4.2.4 雙邊拉普拉斯變換,傅立葉變換與拉普拉斯變換的關係4.3 線性定常系統的頻率特性函式與頻域分析4.3.1 頻率特性函式及其與傳遞函式的關係...
4.1.2雙邊拉普拉斯變換4.1.3拉氏逆變換4.2拉氏變換求解法4.2.1微分方程的求解4.2.2電路的s域分析法4.3系統函式及s平面分析4.3.1時域特性與頻響特性的分析...
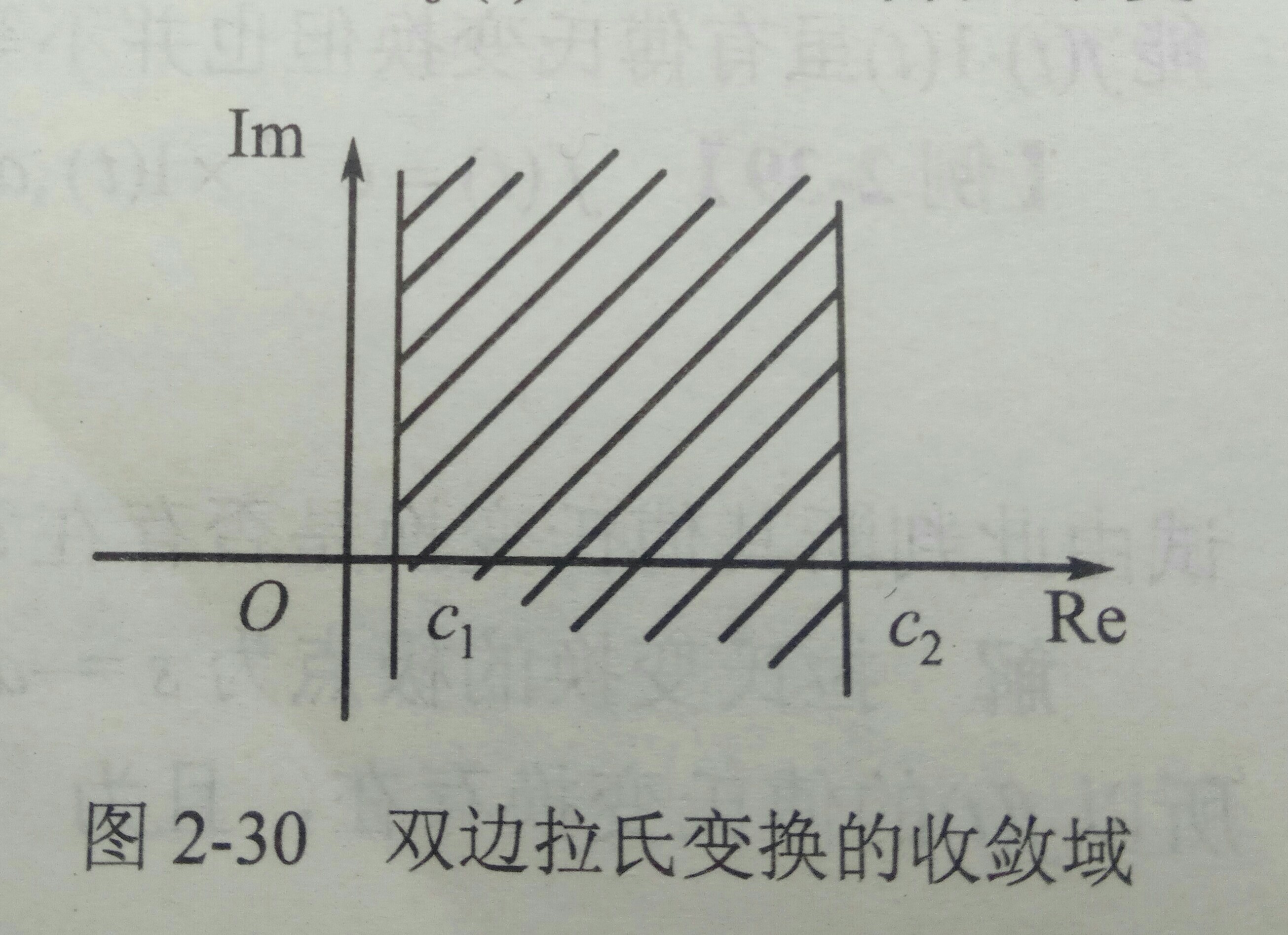
3.2雙邊拉普拉斯變換3.2.1LTI系統的特徵函式3.2.2收斂域3.3單邊拉普拉斯變換3.4單邊拉普拉斯變換的性質3.4.1線性3.4.2微分3.4.3積分...
4.1.1 從傅立葉變換到雙邊拉普拉斯變換 1254.1.2 單邊拉普拉斯變換 1264.1.3 常用函式的拉氏變換對 128思考題 129 [1] 4.2 單邊拉普拉斯變換的重要性質 130...
6.7.2雙邊拉普拉斯變換的性質6.7.3雙邊拉普拉斯逆變換6.8LTI系統的系統函式及其性質6.8.1系統函式6.8.2系統的因果性與穩定性6.8.3可逆性...
4.1 拉普拉斯變換4.1.1 從傅立葉變換到拉普拉斯變換4.1.2 雙邊拉普拉斯變換的收斂域4.1.3 單邊拉普拉斯變換4.1.4 常用信號的單邊拉普拉斯變換...
第5章 拉普拉斯變換及連續系統的 s 域分析1675.1 拉普拉斯變換 1675.1.1 從傅立葉變換到雙邊拉普拉斯變換 1675.1.2 收斂域 168...
§5.5 拉普拉斯反變換§5.6 拉普拉斯變換的基本性質§5.7 線性系硫的拉普拉斯變換分析法§5.8 雙邊拉普拉斯變換§5.9 線性系統的模擬...
第8章連續時間信號的拉普拉斯變換2028 1雙邊拉普拉斯變換2038 2單邊拉普拉斯變換2068 3單邊拉普拉斯變換的特性2098 4周期信號的拉普拉斯變換218...
4.1 拉普拉斯變換 (96)4.1.1 雙邊拉普拉斯變換 (96)4.1.2 單邊拉普拉斯變換 (98)練習題 (100)4.2 拉普拉斯變換的性質 (100)4.2.1 線性性質 (100)...
9.1 拉普拉斯變換2899.1.1 從傅立葉變換到雙邊拉普拉斯變換2899.1.2 單邊拉普拉斯變換2909.1.3 常用函式的拉氏變換對292思考題2939.2 單邊拉普拉斯變換的重要性質293...
