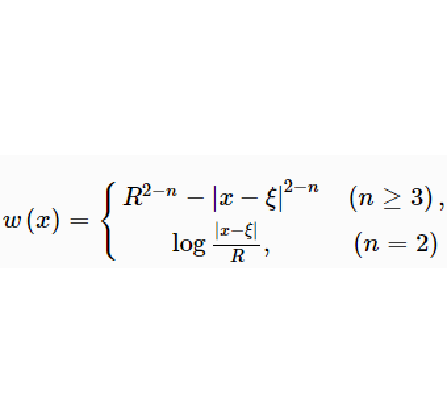閘函式(barrier function)是用來界定區域邊界性狀的一種函式。又稱障礙函式。處理最佳化問題時,在極值點的搜尋過程中,為保證搜尋始終在可行域內,對企圖從可行域內部穿越邊界的點,在目標函式中加入障礙項,表示障礙項的函式即為閘函式。距邊界越近,障礙越大,當趨於邊界時,障礙趨於無窮大,從而保證最優解不會超出可行域。
基本介紹
- 中文名:閘函式
- 外文名:barrier function
- 套用:用來界定區域邊界性狀
- 相關概念:正則邊界點、狄利克雷問題等
基本介紹,正則邊界點,相關定理,
基本介紹
閘函式(barrier function)是用來界定區域邊界性狀的一種函式。設 是
是 上一點,如果
上一點,如果 中存在函式
中存在函式 滿足條件:
滿足條件:




1. 在
在 中是上調和的;
中是上調和的;


2.在 中,
中,



正則邊界點







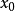



1. 在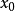 存在閘函式,即存在
存在閘函式,即存在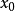 的開鄰域N及
的開鄰域N及 內的上調和函式w>0,使得
內的上調和函式w>0,使得
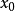
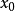


2. 對1.中 的格林函式G,有
的格林函式G,有



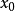
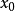
相關定理
定理1設 為區域
為區域 的邊界,
的邊界, 在
在 上連續。如果點
上連續。如果點 是一個正規邊界點,則函式
是一個正規邊界點,則函式









定理2 設 為區域
為區域 的邊界,
的邊界, 在
在 上連續,如果
上連續,如果 上的每一個點都是正規邊界點,則Dirichlet問題
上的每一個點都是正規邊界點,則Dirichlet問題






由定理2 可知,求解Dirichlet問題就轉化為當 滿足什麼條件時,
滿足什麼條件時, 上的每一點都是正規邊界點。這裡給出一種簡單而常見的情況:如果
上的每一點都是正規邊界點。這裡給出一種簡單而常見的情況:如果 在點
在點 處滿足外球條件,且外球的球心為
處滿足外球條件,且外球的球心為 ,則
,則