基本介紹
- 中文名:正則點
- 外文名:regular point
- 所屬領域:微積分
定義

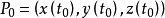
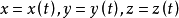




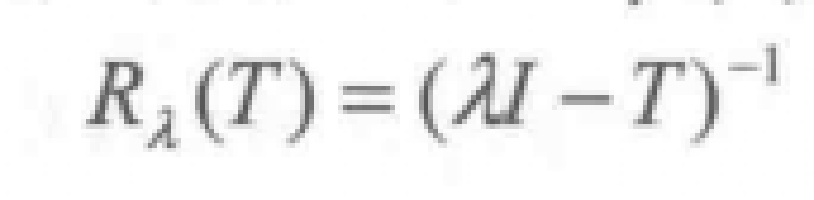

設P為係數取自交換體K中含兩個未定元的多項式.以P(x,y)=0為方程的代數曲線上的點稱為是正則的,如果P在該點的微分不為零. 當K=R時,所考察的代數曲線在這樣點的鄰域上是R^2的一個子流形. 前面的定義立刻能推廣到代數超曲面上.
相關定理
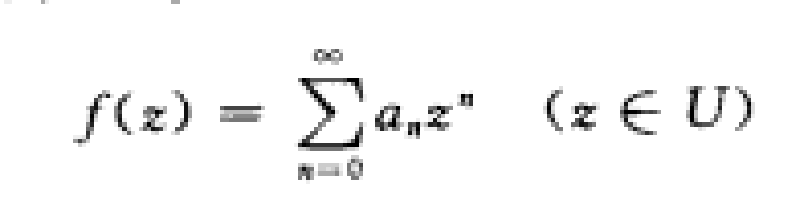

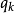
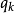

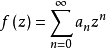

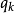



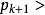




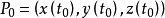
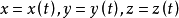




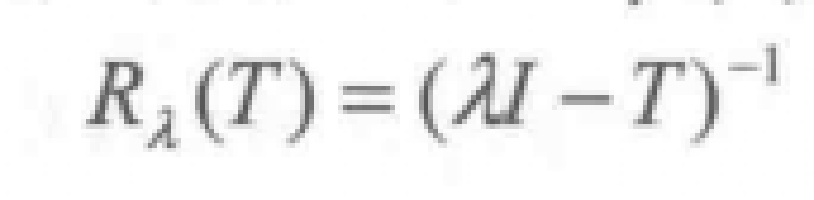

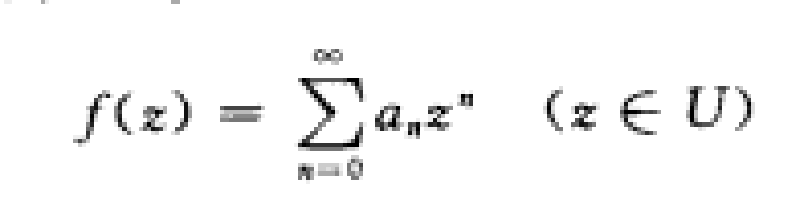

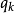
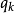

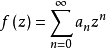

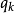



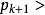


正則點是微積分中的一個重要概念,它用來描述曲線或曲面的“光滑程度”。令D為一開圓盤,假設f∈ H(D),β為D的一個邊界點.若存在中心在β的圓盤D1及函式g∈...
α正則點(α-regular point)是位勢論的一個概念。2(非)正則點常稱為(非)正則點。...... α正則點(α-regular point)是位勢論的一個概念。2(非)正則點常...
映射正則點(regular point of map)微分流形上一類特殊的點.指微分流形上的那種點,可微映射在該點處是淹沒映射。...
正則表達式,又稱規則表達式。(英語:Regular Expression,在代碼中常簡寫為regex、regexp或RE),計算機科學的一個概念。正則表達式通常被用來檢索、替換那些符合某個模式...
正則化(regularization),是指線上性代數理論中,不適定問題通常是由一組線性代數方程定義的,而且這組方程組通常來源於有著很大的條件數的不適定反問題。大條件數...
為方便正則表達式記憶的口訣,口訣描述了正則表達式的書寫規則和常用方法...... 為方便正則表達式記憶的口訣,口訣描述了正則表達式的書寫規則和常用方法 目錄 1 正則表達...
對於完整保守系統,用廣義坐標qi和廣義動量pi(i=1,2,…,N)聯合表示受理想約束的完整保守系統的動力方程。又稱哈密頓正則方程。...
正則函式又稱全純函式、解析函式,屬於高等數學中的函式,可展開為冪級數的(實變)函式,稱為正則函式,上述定義還適合於複變函數。通常,正則函式是對複變函數定義的...
在訓練數據不夠多時,或者overtraining時,常常會導致過擬合(overfitting)。正則化方法即為在此時向原始模型引入額外信息,以便防止過擬合和提高模型泛化性能的一類方法...
正則化是通過對學習算法的修改,如在原約束函式上添加額外的約束和懲罰,改善模型在測試集上的表現,達到減少泛化誤差、提高模型泛化能力的目的的技術。在實際的深度...
正則系統是以傳遞函式收斂於一個常數的前提下,在狀態方程描述的系統中根據直接傳送陣D的不同判斷,特點是s趨於無窮。...
正則條件是指在陳述某一個定理時,常常需要限定這些定理的使用範圍。如果超出這個範圍,則會導致定理所描述的內容不成立。用於限定這個使用範圍的限定條件被稱為“正則...
正則子流形是特殊的子流形,設微分流形N的子流形為M,如果是一個同胚,那么稱M是N的正則子流形,並稱為M在N中的正則嵌入。...
在數論中,正則素數的概念首先由恩斯特·庫默爾在1847年為了處理費馬最後定理而引入。它具有許多種等價的定義方式。...
重慶市璧山區正則中學,原名璧山區城關中學,2002 年12月更名。校訓:正人生,則志成。...... 重慶市璧山區正則中學,原名璧山區城關中學,2002 年12月更名。 校訓:正...
正則波萊爾測度(regular Borel measure)是正則的波萊爾測度。設Ω是豪斯多夫空間。如果μ是B(Ω)上的波萊爾測度且是正則的,則稱μ是B(Ω)上的正則波萊爾測度。...
正則測度(regular measure)一種比較規則的測度。既外正則又內正則的測度稱為正則測度。測度,是數學術語,釋義是構造一個集函式,它能賦予實數集簇М中的每一個集合...
要理解什麼是二叉樹正則,必須了解樹、有向樹、根樹、叉樹等概念。 一個連通且無迴路的無向圖,稱為樹。如果有向圖在不考慮邊的方向時,是一棵樹,那么這個有...
正則模態分析,在常規中,研究結構動力特性一種方法,一般套用在工程振動領域。其中,模態是指機械結構的固有振動特性,每一個模態都有特定的固有頻率、阻尼比和模態振型...
