基本介紹
- 中文名:邊邊邊定理
- 外文名:Theorem of edges and edges
- 作用:證明兩個三角形全等
- 解釋:有三邊對應相等的兩個三角形全等
- 簡稱:SSS
- 證明者:歐幾里德
定義,證明方法,方法1,方法2,定理的證明,
定義
《義務教育數學課程標準》(2011 版)將判定三角形全等中的“邊邊邊”列為基本事實,即作為證明推理的出發點,並不要求證明。同時,為了幫助學生髮現並理解這條基本事實的合理性,現行教材大都沿襲傳統做法,即通過尺規作圖,根據已知三邊的長度作出一個三角形,再將作出的三角形與原三角形放在一起,看是否重合來得到“邊邊邊”的合理性。以上做法是實驗幾何的方法,並沒有證明“邊邊邊”的成立。
證明方法
歐幾里得的《幾何原本》,其中命題 8 證明了三邊分別相等的兩個三角形,則夾在等邊中間的角也相等。書中採用的是反證法,並且藉助書中另外一條定理(即命題 7)來完成證明。有了這條定理做保證,就可以繼續藉助“邊角邊”完成“邊邊邊”的證明。
方法1
設:在三角形ABC和三角形DEF中,AB等於DE,AC等於DF,即AB是DE的對應邊,AC是DF的對應邊。BC等於EF。

那么說:三角形ABC全等於三角形DEF。
將點B替換成點E,線段BC替線段EF,因為BC等於EF,所以點C與點F重合,那么BA、AC分別於ED、DF重合。
如果底邊BC與底邊EF重合,而BA、AC兩邊與ED、DF兩邊不重合,形成了新的兩邊與EG、FG重合,那么從一條線段的兩個末端引出的兩條線段相交於一點,同一條線段的兩個末端引出的另外兩條線段交與另一點,兩組對應邊不能相等。所以:假設不能成立。
所以三角形ABC和三角形DEF可以重合,所以三角形ABC和三角形DEF全等。
方法2
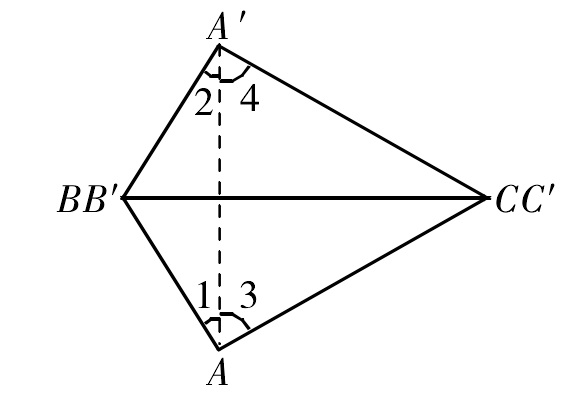
一般證明“邊邊邊”常採用以下方法: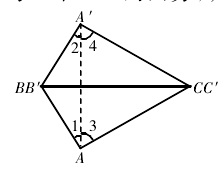 圖1
圖1
 圖1
圖1在△ABC和△A'B'C'中,已知AB=A'B',AC=A'C',BC=B'C'。求證:△ABC ≌ △ A'B'C'。
證明:將△ABC通過平移、旋轉和軸反射,使BC的像與B'C'重合(並使A的像與A'在BC的兩旁),連線AA',得到圖1。
因為AB=A'B',AC=A'C',
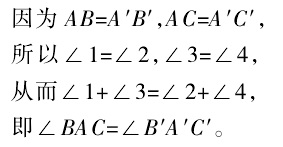
在△ABC和△A‘B'C'中,AB=A‘B',角BAC=角B'A'C',AC=A'C',所以△ABC ≌ △ A'B'C' ( SAS )。
由此得到以下基本事實:三邊對應相等的兩個三角形全等。注意到上述證明過程中,藉助了“等腰三角形等邊對等角”這一定理,儘管課標對“邊邊邊”不作證明要求,但從幾何定理的編排順序以及數學教材的嚴謹性來講,在呈現“邊邊邊”這一基本事實之前,最好先證明等腰三角形的相關性質,再介紹“邊邊邊”,那么一切將順理成章。
定理的證明
藉助“邊角邊”證明“等邊對等角”:
(1)歐幾里得的《幾何原本》的命題 5 也是證明等腰三角形“等邊對等角”。已知AB=AC,延長AB到D,延長AC到E,使AD=AE。由《幾何原本》命題 4 的“邊角邊”,可證明△ADC≌△AEB,從而BE=CD,角BDC=角BEC,又BD=CE,再用“邊角邊”可證得△DBC≌△ECB,進 而得 到角DBC=角ECB,於是角ABC=角ACB。
這個證明過程要用到兩次全等證明,這對於初學者來說很難。因此該定理戲稱為“笨蛋的難關(Asses' Bridge)”,照原文直譯即“驢橋”,意思是學完該定理的證明,學習者就基本掌握證明的方法了。
(2)還有一種證明方法是證明“自己與自己全等”。如圖 2,已知△ABC,AB=AC。因為AB=AC,角A=角A,AC=AB,所以△ABC≌△ACB,所以角B=角C。這種證明方法巧妙,但一般的人很難接受這種證明方式。 圖2
圖2
 圖2
圖2以上這些證明方式都是利用“邊角邊”完成證明,也就是說教材可以先講“邊角邊”,再證明等腰三角形的相關性質,接著就可以推出“邊邊邊”了。考慮到等腰三角形的知識點比較多(含性質和判定),從教材編寫的角度考慮,單獨將“等腰三角形”做一小節是合適的。